|
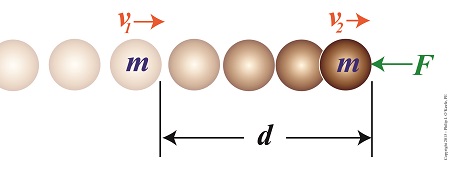
My work as an engineering expert sometimes involves computations of energy expended, as when I must determine how much energy is required to move something. But sometimes the opposite needs to be calculated, that is, how much energy is required to stop something already in motion. That’s the subject of today’s discussion, which we’ll approach by way of the Work-Energy Theorem. The Work-Energy Theorem states that the work required to slow or stop a moving object is equal to the change in energy the object experiences while in motion, that is, how its kinetic energy is reduced or completely exhausted. Although we don’t know who to attribute the Theorem to specifically, we do know it’s based on the previous work of Gaspard Gustave de Coriolis and James Prescott Joule, whose work in turn built upon that of Isaac Newton’s Second Law of Motion. Consider the example shown here. A ball of mass m moves unimpeded through space at a velocity of v1 until it is met by an opposing force, F. This force acts upon the ball over a travel distance d, resulting in the ball’s slowing to a velocity of v2. The Work – Energy Theorem Illustrated
Does the illustration make clear the Work-Energy Theorem dynamics at play? If not, return for the second part of this blog, where we’ll clarify things by getting into the math behind the action. Copyright 2015 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |
Tags: energy, engineering expert witness, Gaspard-Gustave de Coriolis, Isaac Newton's Second Law of Motion, James Prescott Joule, kinetic energy, moving object, work, work-energy theorem