|
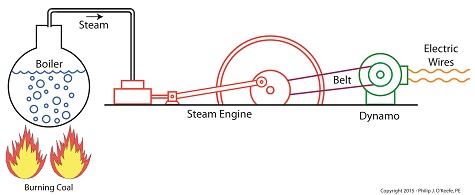
In my work as an engineering expert I’ve dealt with all forms of energy, just as we’ve watched James Prescott Joule do. He constructed his Joule Apparatus specifically to demonstrate the connection between different forms of energy. Today we’ll see how he furthered his discoveries by building a prototype power plant capable of producing electricity, a device which came to be known as Joule’s Experiment With Electricity. Joule’s Experiment With Electricity As the son of a wealthy brewer, Joule had been fascinated by electricity and the possibility of using it to power his family’s brewery and thereby boost production. To explore the possibilities, he went beyond the Apparatus he had built earlier and built a device which utilized electricity to power its components. The setup for Joule’s experiment with electricity is shown here. Coal was used to bring water inside a boiler to boiling point, which produced steam. The steam’s heat energy then flowed to a steam engine, which in turn spun a dynamo, a type of electrical generator. Tracing the device’s energy conversions back to their roots, we see that chemical energy contained within coal was converted into heat energy when the coal was burned. Heat energy from the burning coal caused the water inside the boiler to rise, producing steam. The steam, which contained abundant amounts of heat energy, was supplied to a steam engine, which then converted the steam’s heat energy into mechanical energy to set the engine’s parts into motion. The engine’s moving parts were coupled to a dynamo by a drive belt, which in turn caused the dynamo to spin. Next time we’ll take a look inside the dynamo and see how it created electricity and led to another of Joule’s discoveries being named after him. Copyright 2015 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |
Posts Tagged ‘forensic engineer’
Joule’s Experiment With Electricity
Friday, October 16th, 2015James Prescott Joule and the Joule Apparatus
Tuesday, October 6th, 2015|
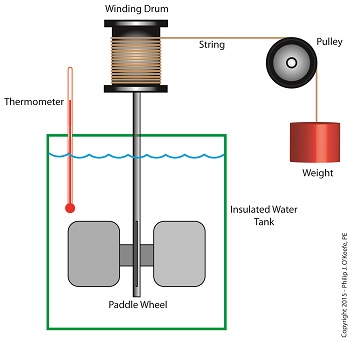
As an engineering expert I’ve often witnessed energy change forms, something our example coffee mug has been experiencing as it moves from a shelf to the floor. The mug’s various energies were proven to be mathematically equivalent, expressed as, 4.9 kg•meter2 /second2 , which is read as, “kilogram meter squared per second squared.” This mouthful led to the renaming of the measurement to the Joule, in honor of James Prescott Joule, a scientist who successfully demonstrated the interrelationship between different forms of energy. We’ll focus on one of his experiments, the Joule Apparatus, today. Back in the 1840s Joule built his Apparatus, a device which demonstrated the interrelationship between different forms of energy. The Joule Apparatus The Joule Apparatus consisted of a weight suspended by string over a pulley, which in turn was wound around a winding drum. As long as the drum remained stationary, the weight remained motionlessly suspended. While motionless, the weight’s potential energy lay latent within it, just as it had in our example coffee mug resting on a shelf. But when the pressure keeping the winding drum stationary was released, the weight was set free to fall, and its potential energy began converting to kinetic. In the process, the string the weight was attached to unwound from the drum, which caused the drum to turn and along with it the paddle wheel it was attached to. Joule’s Apparatus followed energy through many forms. From the quiet of potential energy to the kinetic energy demonstrated by the falling weight. The kinetic energy in turn was converted into mechanical energy, made manifest by the interaction between the moving drum and paddle wheel. The rotating paddles agitated the water, causing its temperature to rise. Observing this, Joule concluded that the mechanical energy of the spinning paddle wheel had been converted into heat energy, which temperature measurement proved was transferred into the water. Joule’s experiment thus proved the link between potential, kinetic, mechanical, and heat energies. Joule’s work paved the way to make possible the later development of a host of modern mechanical devices that also converted heat energy into mechanical energy, or vice versa. These devices include a car’s engine and your kitchen’s refrigerator. Next time we’ll see how Joule demonstrated a link between electrical and other forms of energy, including mechanical and heat. We’ll then use his discoveries to convert our falling coffee mug’s kinetic energy into yet another form. Copyright 2015 – Philip J. O’Keefe, PE Engineering Expert Witness Blog
____________________________________ |
Willem Gravesande’s Experimentation on Kinetic Energy
Friday, September 11th, 2015|
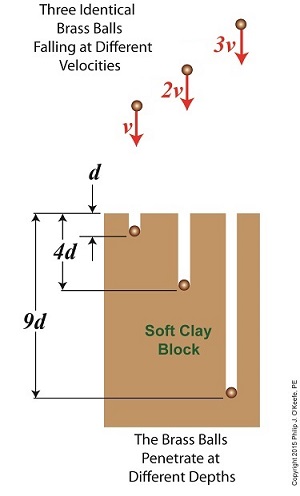
Last time we introduced The Law of Conservation of Energy, which holds that energy can neither be created nor destroyed. We then applied the concept to a mug resting on a shelf, brimming with latent gravitational potential energy. Today we’ll continue our discussion with a focus on kinetic energy and how Willem Gravesande’s experimentation contributed to our understanding of the subject. The concept of kinetic energy was first posited by mathematicians Gottfried Leibniz and Johann Bernoulli in the early 18th Century when they theorized that the energy of a moving object is a factor of its mass and speed. Their theory was later proven by Willem Gravesande, a Dutch lawyer, philosopher, and scientist. Gravesande conducted experiments in which he dropped identical brass balls into a soft clay block. See Figure 1. Figure 1 Figure 1 shows the results obtained when balls of the same mass m are dropped from various heights, resulting in different velocities as they fall and different clay penetrations. The ball on the left falls at velocity v and penetrates to a depth d. The center ball falls at twice the left ball’s velocity, or 2v, and penetrates four times as deep, or 4d. The right ball falls at three times the left ball’s velocity, 3v, and it penetrates nine times deeper, 9d. The results indicate an exponential increase in clay penetration, dependent on the balls’ speed of travel. In fact, all the kinetic energy that the balls exhibited during freefall was converted into mechanical energy from the instant they impacted the clay until their movement within it stopped. This change in forms of energy from kinetic to mechanical demonstrates what Julius Robert von Mayer had in mind when he derived his Law of Conservation of Energy. For a refresher on the subject, see last week’s blog, The Law of Conservation of Energy. As a result of his experimentation, Gravesande was able to conclude that the kinetic energy of all falling objects is a factor of their mass multiplied by their velocity squared, or m × v2. We’ll see next time how Gravesande’s work paved the way for later scientists to devise the actual formula used to calculate kinetic energy and then we’ll apply it all to our coffee mug falling from the shelf. Copyright 2015 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________
|
Computing Potential Energy
Tuesday, August 25th, 2015|
Last week we discovered that objects acquire potential energy as it relates to gravity based on the height those objects are elevated above the ground. We also introduced an equation to calculate the potential energy of a coffee mug perched on a shelf. We’ll work with that equation today and compute the latent energy that’s hidden within that mug. Here again is the equation to determine potential energy, put in terms relating to gravity, PEgravitational = m × g × h where m is the mass of the mug, h is the height it’s been elevated above the floor, and g is the Earth’s acceleration of gravity factor, as explained in my previous blog entitled, Sir Isaac Newton and the Acceleration of Gravity. The equation above can be solved using either English or metric units. In the US it’s generally standard practice to perform calculations using English units, such as feet and pounds. But when measuring mass a less familiar English unit, the slug, comes into play. If you’re interested in learning more about this unit, go to a previous blog article entitled, The Force of Gravity. The kilogram is the metric equivalent of a slug. Since it’s the unit of mass most commonly used throughout the world, we’ll use it to perform our calculation. Let’s say our mug has a mass of 0.25 kilograms, the shelf it’s resting on is 2 meters above the floor, and g is 9.8 meters/second2. The mug’s gravitational potential energy would then be expressed as, PEgravitational = (0.25 kg) × (9.8 meters/second2) × (2 meters) PEgravitational = 4.9 kg • meter2/second2
Next time we’ll expand on our discussion of potential energy and discuss the Law behind the phenomenon and the fact that energy can only be converted from one form to another. Copyright 2015 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________
|
Gravitational Potential Energy on Earth
Monday, August 17th, 2015|
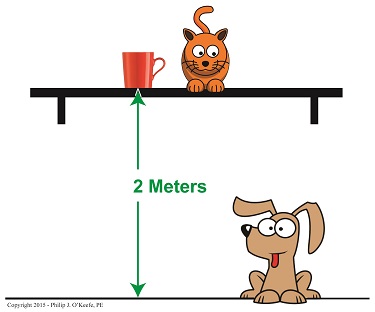
Last week we concluded our discussion on the force of gravity within our solar system. Today we’ll turn our attention to the subject of gravity on Earth and exploring the physics behind falling objects. We’ll start off by discussing potential energy as it relates to gravity, or the latent energy acquired by an object when it’s been elevated above ground level. Potential energy was the term adopted by 19th Century Scottish scientist William Rankine to represent the latent, or masked, energy hidden within objects. As an example, let’s say you’ve placed your favorite coffee mug in its designated spot on the kitchen shelf. Sitting there so still you wouldn’t dream it was brimming with gravitational potential energy, but if your cat came along and brushed against it, sending it freefalling to the floor, your mug would quickly become a projectile, gaining speed at a uniform rate as it accelerated towards ground level. Where did that once passive little cup acquire its mounting energy? Simply by virtue of the fact it had been lifted by your arm and placed in an elevated position. You see, Earth’s gravitational pull is forever exerting its invisible tug on objects. It was tugging at the mug as you lifted it, and the higher you lifted it, the more gravitational potential energy the mug received. Once perched on the shelf it bridled with latent energy, only to be set free when the cat caused it to lose its support. To illustrate the relationship between the coffee mug, the shelf, and Earth’s gravitational pull, we’ll employ the equation used to compute potential energy, notated in terms of gravity, PEgravitational = m × g × h This equation states that the mug’s gravitational potential energy, PEgravitational, is a factor of its mass, m, Earth’s gravitational pull, g, and the mug’s height above ground level, h. Within the scientific community g is referred to as Earth’s acceleration of gravity, a phenomenon commonly accepted to be the uniform accelerating rate at which an object falls on Earth, equal to 9.8 meters per second per second, or meters/second2. It represents a rate of constant acceleration, which happens to be precisely the same whether the object falling is a brick, feather, or coffee mug. Next time we’ll work with the potential energy equation which will enable us to see how the curious orange kitty sets loose the latent power held within that mug. Copyright 2015 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________
|
The Sun’s Gravitational Force
Monday, August 3rd, 2015|
Last time we discovered that Earth zips around the sun at the mind boggling speed of 29,680 meters per second. This is the final bit of information required to calculate Fg, the gravitational force exerted upon Earth by its sun, as set out in Newton’s equation on the subject and derived from his Second Law of Motion. We’ll calculate that quantity today. Newton’s formula that we’ll be working with is, Fg = [m × v2] ÷ r where Earth’s speed, or orbital velocity, is the v in the equation. The other variables, m and r, have previously been determined in this blog series. For a refresher see Centripital Force Makes the Earth Go Round, What is Earth’s Mass, and Calculating the Distance to the Sun. Earth’s mass, m, is valued at 5.96 × 1024 kilograms, while r is Johannes Kepler’s astronomical unit, equal to about 149,000,000,000 meters. Inserting these numerical values into Newton’s equation to determine the sun’s gravitational force acting upon Earth we arrive at, Fg = [(5.96 × 1024 kilograms) × (29,680 meters per second)2] ÷ 149,000,000,000 meters Fg = 3.52 × 1022 kilogram • meter per second2 This metric unit of force, kilogram • meter per second2, represents kilograms multiplied by meters, and their product divided by seconds squared. It’s known in scientific circles as the Newton, in honor of Sir Isaac Newton, widely recognized as one of the greatest scientists of all time and a key figure in the scientific revolution that began over three centuries ago. Therefore the sun’s gravitational force acting upon Earth is typically referred to as, Fg = 3.52 × 1022 Newtons Here in the US where we like to use English units such as feet and pounds, the Newton is said to equal 0.225 pounds of force. Therefore in English units the sun’s gravitational force is expressed as, Fg = (3.52 × 1022 Newtons) × (0.225 pounds of force per Newton) Fg = 7.93 × 1021 pounds That’s scientific notation for 7,930,000,000,000,000,000,000 pounds! That’s the amount of force exerted by the sun’s gravitational pull on Earth. Seems about right — right? Now that we know Fg, we have everything we need to calculate the mass of the sun, which in turn enables us to determine the mass and gravity of other planets in our solar system. We’ll calculate the sun’s mass next time. ____________________________________
|
Earth’s High Speed Race Around the Sun
Tuesday, July 28th, 2015|
Last time we began our discussion on velocity by focusing on one of its aspects, distance, and we calculated Earth’s orbital distance around the sun to be 5,816,023,200 miles. Today we’ll focus on velocity’s other aspect, time. Together, these aspects will allow us to solve for Earth’s orbital velocity, aka speed. When early astronomers monitored Earth’s journeys, they found it took exactly one year for it to complete its orbit around the sun. They combined this fact with Earth’s orbital travel distance of 5,816,023,200, or 9.36 × 1011 meters — meters being the unit of measurement most often used in scientific computations — and solved for Earth’s orbital velocity as follows, v = 9.36 × 1011 meters ÷ 1 year = 9.36 × 1011 meters per year The scientific notation of 9.36 × 1011 equates to 936,000,000,000 meters, a large and unruly number to work with. We can simplify things further by breaking this number down into units of meters per second, which will then allow us to arrive at Earth’s velocity in terms of miles per hour, something most Earthlings can relate to. One meter per second is equal to 2.237 miles per hour, and there are 31,536,000 seconds in one year, so breaking Earth’s orbital velocity down into meters per second we arrive at, v = 9.36 × 1011 meters ÷ 31,536,000 seconds = 29,680 meters per second v = (29,680 meters per second) × (2.237 mph/m/sec) = 66,394 miles per hour Yes, it’s true, Earth whips around the sun at warp speed. Our fastest man made rockets only achieve speeds of about 25,000 miles per hour. Earth beats them two-to-one! Now that we know Earth’s orbital velocity, we have everything we need to calculate the gravitational force exerted on Earth by the sun. We’ll do that next time.
____________________________________
|
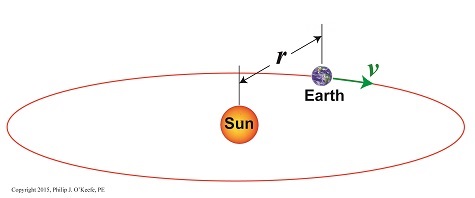
Earth’s Orbital Velocity
Sunday, July 19th, 2015|
Last time we introduced Newton’s equation to calculate the sun’s gravitational force acting upon Earth, and today we’ll begin solving for the last remaining unsolved variable within that equation, v, Earth’s orbital velocity. Here again is Newton’s equation, Fg = [m × v2] ÷ r For a refresher on how we solved for m, Earth’s mass, and r, the distance between Earth and the sun, follow these links to past blogs in this series, What is Earth’s Mass and Calculating the Distance to the Sun. Velocity, or speed, as it’s most commonly referred to, is based on both time and distance. To bear this out we’ll use an object and situation familiar to all of us, traveling in a car. The car’s velocity is a factor of both the distance traveled and the time it takes to get there. A car traveling at a velocity of 30 miles per hour will cover a distance of 30 miles in one hour’s time. This relationship is borne out by the formula, vCar = distance traveled ÷ travel time vCar = 30 miles ÷ 1 hour = 30 miles per hour Similarly, v is the distance Earth travels during its orbital journey around the sun within a specified period of time. It had been observed since ancient times that it takes Earth one year to complete one orbit, so all that remained to be done was calculate the distance Earth traveled during that time. Vital to calculations was the fact that Earth’s orbit is a circle, which allows geometry to be employed and calculations to be thereby simplified. Refer to Figure l. Figure 1 From geometry we know that the circumference of a circle, C, is calculated by, C = 2× π × r where π is a constant, the well known mathematical term pi, which is equal to 3.1416, and r is the radius of Earth’s circular orbit, determined, courtesy of the work of Johannes Kepler and Edmund Halley, to be approximately 93,000,000 miles. Stated in metric units, the unit of measurement most often employed in science, that comes to 149,000,000,000 meters. Inserting these numerical values for π and r into the circumference formula, scientists calculated the distance Earth travels in one orbit around the sun to be, C = 2 × π × 149,000,000,000 meters = 9.36 x 1011 meters Next time we’ll introduce the time element into our equations and solve for v, and from there we’ll go on and finally solve for Fg, the sun’s gravitational force acting upon Earth.
____________________________________
|
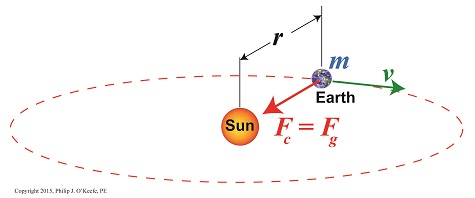
Centripetal Force Makes the Earth Go Round
Thursday, July 9th, 2015|
Last time we saw how centripetal force is responsible for keeping a child’s ball moving in a circular path when twirled above his head. Today we’ll see how that same force is responsible for keeping Earth in its rotation around the sun. We’ll use Isaac Newton’s Second Law of Motion as it relates to centripetal force to bear that out today. Our example from last week, Figure 1 According to Newton’s Second Law of Motion, Fc, the centripetal force acting upon the ball, is calculated by the equation, Fc = [mball × v2] ÷ rstring where, mball is the ball’s mass, v the ball’s velocity, and rstring is the length of the string. The mechanics are obviously different with regard to Earth and its orbit around the sun, where there’s no obvious physical link between the objects in rotation. In this case the sun’s gravitational force, Fg, acts to tether Earth to it. And just like the string and ball, the sun’s gravitational tether creates a centripetal force, Fc, which prevents Earth from leaving its orbital path. See Figure 2. Figure 2 Newton concluded that for the Earth to remain on its permanent, fixed path of orbit around the sun, Fc must be equal to Fg, and that the forces in play between the sun and Earth were like a gigantic tug of war where neither side is able to pull any harder than the other. This stalemate is responsible for keeping Earth stably in place in its orbit. According to Newton’s Second Law, the sun’s gravitational force acting upon the Earth is calculated by, Fg = Fc = [m × v2] ÷ r where, m is Earth’s mass, v its orbital velocity, and r the distance between Earth and the sun. Thanks to early scientists like Edmund Halley and Henry Cavendish, the values for m and r had already been determined. That left v, Earth’s orbital velocity, the only variable remaining to be solved. We’ll see how 19th Century scientists accomplished that next time.
____________________________________
|
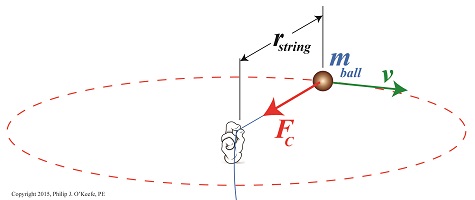
Centripetal Force
Friday, July 3rd, 2015|
Have you ever wondered how Earth keeps its steady orbit around its life sustaining sun, or what prevents it from breaking away and flying off willy-nilly into the universe? It’s more than just simple gravity, it’s the physics behind centripetal force, the topic we’ll be exploring today. We’ve been working our way towards a full discussion on gravity in this long blog series, navigating subjects such as the behavior of falling objects, the acceleration of gravity, the masses of Earth and the sun, and the optical measurement of cosmic distances. We’ve now come full circle from my opening blog on the subject, Gravity and the Mass of the Sun. In that blog an equation was introduced as a means to calculate the mass of the sun, and in that equation is the variable we’ll be working towards solving today, Fg, the sun’s gravitational force upon the Earth. Here again is that equation, M = (Fg × r2) ÷ (m × G) Gravity, mass, and distance all come into play in forming the structure of our universe, and the variables in this equation reflect that: M, the mass of the sun, r the distance between Earth and the sun, m the Earth’s mass, and G the universal gravitational constant. With the exception of Fg, all variables in this equation have already been solved for in previous blogs in this series. For a refresher go to, Calculating the Distance to the Sun, What is Earth’s Mass? and Newton’s Law of Gravitation and the Universal Gravitational Constant. As there is no direct means to measure the cosmic quantity, Fg, we’re left to an indirect method for its computation. The indirect method is based on the phenomenon of centripetal force, Fc something most children become acquainted with when they experience the thrill of twirling an object attached to a string, say a rubber ball, above their heads. See Figure 1. Figure 1 As the ball is twirled, the string becomes taut. The energy exerted upon it by the child’s hand, coupled with the ball’s mass and traveling speed/velocity, v, make the ball want to move off in a straight trajectory into space, like a launched projectile. But the string it’s attached to prevents it from doing so, forcing the ball to instead travel a circular path around the center point of rotation. The taut string and the ball’s circular path are evidence of centripetal force, Fc, at work. Next time we’ll employ Isaac Newton’s Second Law of Motion to the centripetal force phenomenon to see how the sun’s gravitational force keeps Earth in a stable circular orbit around the sun.
____________________________________
|