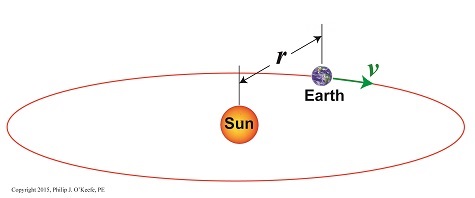
|
Last time we introduced Newton’s equation to calculate the sun’s gravitational force acting upon Earth, and today we’ll begin solving for the last remaining unsolved variable within that equation, v, Earth’s orbital velocity. Here again is Newton’s equation, Fg = [m × v2] ÷ r For a refresher on how we solved for m, Earth’s mass, and r, the distance between Earth and the sun, follow these links to past blogs in this series, What is Earth’s Mass and Calculating the Distance to the Sun. Velocity, or speed, as it’s most commonly referred to, is based on both time and distance. To bear this out we’ll use an object and situation familiar to all of us, traveling in a car. The car’s velocity is a factor of both the distance traveled and the time it takes to get there. A car traveling at a velocity of 30 miles per hour will cover a distance of 30 miles in one hour’s time. This relationship is borne out by the formula, vCar = distance traveled ÷ travel time vCar = 30 miles ÷ 1 hour = 30 miles per hour Similarly, v is the distance Earth travels during its orbital journey around the sun within a specified period of time. It had been observed since ancient times that it takes Earth one year to complete one orbit, so all that remained to be done was calculate the distance Earth traveled during that time. Vital to calculations was the fact that Earth’s orbit is a circle, which allows geometry to be employed and calculations to be thereby simplified. Refer to Figure l.
Figure 1 From geometry we know that the circumference of a circle, C, is calculated by, C = 2× π × r where π is a constant, the well known mathematical term pi, which is equal to 3.1416, and r is the radius of Earth’s circular orbit, determined, courtesy of the work of Johannes Kepler and Edmund Halley, to be approximately 93,000,000 miles. Stated in metric units, the unit of measurement most often employed in science, that comes to 149,000,000,000 meters. Inserting these numerical values for π and r into the circumference formula, scientists calculated the distance Earth travels in one orbit around the sun to be, C = 2 × π × 149,000,000,000 meters = 9.36 x 1011 meters Next time we’ll introduce the time element into our equations and solve for v, and from there we’ll go on and finally solve for Fg, the sun’s gravitational force acting upon Earth.
____________________________________
|
Posts Tagged ‘Isaac Newton’
Earth’s Orbital Velocity
Sunday, July 19th, 2015
How Long is a Pendulum’s Swing?
Wednesday, October 29th, 2014|
What would you do to pass the time if you were stuck on a ship of the middle ages for weeks at a time? Dutch mathematician Christiaan Huygens used the time to study the movement of clock pendulums. He watched them for endless hours, and he eventually came to realize that the pendulums’ swing was uneven due to the ship’s listing on the waves, a phenomenon which also affected the ship’s clocks’ accuracy. Eager to devise a solution to the problem of inaccurate time keeping, Huygens dedicated himself to finding a solution to the problem, and in so doing increase the navigational accuracy of ships as well. His efforts eventually resulted in a formula that shared a common variable with Isaac Newton’s gravitational formula, namely, g, Earth’s acceleration of gravity factor, a value which Huygens posited was indeed a non varying constant.
Building upon Newton’s work, Huygens devised a formula which demonstrated the mathematical relationship between the motion of a clock’s pendulum and g. That formula is, T = 2 × ∏ × (L ÷ g)1/2 where, T is the period of time it takes a pendulum to make one complete swing, ∏ the Greek symbol pi, valued at 3.14, and L the length of the pendulum. Since devices capable of directly measuring the Earth’s gravity did not exist then, as they still don’t exist today, how in the world (pardon the pun) was Huygens able to arrive at this formula? Thinking outside the box, he posited that if one knows the length of the pendulum L, and then accurately measures the time it takes for the pendulum to complete its swings, taking into account the varied times that resulted due to the ship’s listing, one can calculate g using his equation. He eventually determined g‘s value to be equal to 32.2 feet per second per second, or 32.2 ft/sec2. Fast forwarding to Henry Cavendish’s time, Huygens’ work with pendulums and his determination of g was well known. We’ll see what Cavendish did with this knowledge next time.
_______________________________________
|
Huygens’ Use of Pendulums
Tuesday, October 21st, 2014|
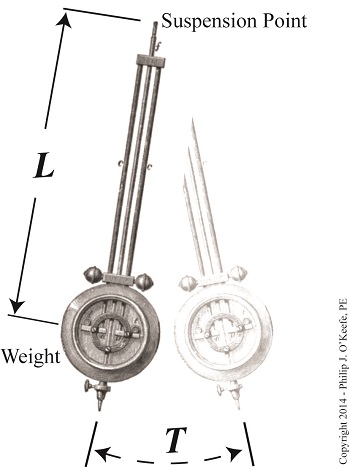
Last time we learned that Henry Cavendish determined a value for G, the universal gravitational constant, fast on his way to determining a quantity he was determined to find, the Earth’s mass. Today we’ll see how the previous work of Christiaan Huygens, a contemporary of Isaac Newton’s, helped him get there. First Cavendish used algebra to rearrange terms in Newton’s gravitational formula so as to solve for M, Earth’s mass. Rearranged, Newton’s formula becomes, M = (g × R2) ÷ G But in order to solve for M, Cavendish first needed to know Earth’s acceleration of gravity, g. To aid him in this calculation he referred back to the work of Christiaan Huygens, a Dutch mathematician from Newton’s time.
Huygens was eager to devise a formula capable of predicting clock pendulums’ motions on ships, his goal being to invent a timepiece accurate enough to make navigating ships easier. He hypothesized that a key factor in predicting a pendulum’s movement was an unknown constant, the acceleration of gravity factor, g, which Newton had previously posited existed. Through meticulous observation, Huygens came to realize that the time it took for pendulums to complete one swing back and forth was dependent not only on the length of the pendulum, but also this unknown quantity. In order for Huygens’ computations to work, the value of g had to be a constant, meaning, its value could not vary between computations; g‘s value was in fact a fudge factor, a phantom he would assign a specific numerical value. Huygens’ needed it in order to make his hypothesis work, a practice commonly use by scientists, even today. Determining a value for g would allow Huygens to successfully relate the length of the pendulum to the timing of its swing and to create a mathematical relationship between them. Huygens ultimately determined g’s value to be a whopping 32.2 feet per second per second, or 32.2 ft/sec2. We’ll see how he did it next time.
_______________________________________
|
How Big is the Earth?
Wednesday, October 8th, 2014|
Last time we discussed Isaac Newton’s Law of Gravitation and how he used it to arrive at conclusions concerning gravity. He theorized the existence of a universal gravitational constant, G, a set numerical value for all heavenly bodies in our universe, and he developed a formula to determine the acceleration of gravity, g. Newton felt sure that the gravity at play on the surface of any heavenly body, such as stars and planets, could be determined if one knew the value of G, along with the object’s mass, M, and radius, R, and he developed this equation to do so, g = (G × M) ÷ R2 At this point you may be thinking, Finding the mass and radius of a heavenly body is hard enough, but what is this universal gravitational constant?? Good point. Back in Newton’s time, the existence of G was purely speculative. He conceived it to be a numerical value which would act as a fudge factor, enabling his equation for determining g to work. As a matter of fact, Newton had no clue of how to determine G and was convinced that it would be beyond anyone’s ability to do so. The mysterious G factor and its numerical value were not actually determined until more than a hundred years later by Henry Cavendish. In 1796 Cavendish was focused on determining the Earth’s mass, M, by using Newton’s equation. To arrive at a value for G, Cavendish conducted experiments which measured the gravitational attraction between two lead spheres attached by way of a torsion balance. After much testing he eventually concluded that he had computed G to a reasonable degree of accuracy and that its value was equal to 3.439 x 10-8 cubic feet per slug per second squared. In this case a slug is not a slimy creature living in the garden, but rather a unit of measurement used to quantify the mass of an object. For the full story, see this article on Cavendish’s experiment by The Physics Classroom. But even after determining G, Cavendish still had to obtain values for g and R in order to calculate M. This was made possible thanks to the work of two men who came before him. One of these was the Greek mathematician Eratosthenes, who way back in 230 B.C. discovered that the radius of the earth, R, could be calculated by simply measuring the shadows of objects cast on Earth’s surface. All he needed was a measuring stick and geometry. For the full story see this fascinating article on the subject from Bucknell University.
As for the value of g, the acceleration of gravity on Earth, Cavendish was aided by the previous efforts of a Dutch mathematician from Newton’s time, Christiaan Huygens. You may recall that Huygens was first introduced in a previous blog series on spur gear geometry, where we learned that he studied the motion of clock pendulums. Through observation, Huygens was able to arrive at a mathematical formula capable of predicting the pendulums’ often erratic motion on ships at sea. Next time we’ll see how Huygens’ insights gained by watching pendulums ultimately made it possible for him to arrive at a numerical value for Earth’s acceleration of gravity, g. _______________________________________
|
Newton’s Law of Gravitation and the Universal Gravitational Constant
Monday, September 29th, 2014|
Last time we introduced the term acceleration of gravity, a physical phenomenon posited by Sir Isaac Newton in his book Philosophia Naturalis Principia Mathematica. Newton’s Law of Gravitation is also presented in this book. It provides the basis for his mathematical formula to calculate the acceleration of gravity, g, for any heavenly body in the universe. Newton’s formula to compute the acceleration of gravity is, g = (G × M) ÷ R2 where, g is the acceleration of gravity, M the mass of the heavenly body, R the radius, and G the universal gravitational constant. As for the values of the variables in his equation, Newton theorized that G would be a constant, holding the same numerical value throughout the universe. This universal gravitational constant would be the glue that bound together M, the mass of the object being measured, and R, its radius, and render Newton’s formula a workable equation. Without these three values, scientists would be unable to determine the acceleration of gravity rate, g, for the heavenly body under study, and Newton’s equation would be useless, relegated to the depths of pure mathematical theory. In fact, the value for G wasn’t determined until 1796. At that time Henry Cavendish derived its value as an adjunct to calculating the mass of Earth. In the end he was able to arrive at values for Earth’s mass, M, as well as its radius, R. He also came up with the much needed value for G, the universal gravitational constant. He was able to accomplish so much by building upon the work of other scientists before him. We’ll see who those earlier scientists were and how they contributed to the world’s discoveries concerning gravity next time.
_______________________________________
|
Mechanical Engineering, Focus on Dynamics, Part II, Kinetics
Monday, November 2nd, 2009|
In Part I of Mechanical Engineering, Focus On Dynamics, we talked about kinematics. This week in Part II, we’ll talk about kinetics. Kinetics is the study of the relationship that exists between forces acting on a body, the mass of the body itself, and its motion. It’s used to predict the motion caused by given forces acting on a body or to determine the forces required to produce a motion of the body. In kinetics forces can be attributed to the motion of an object by way of Sir Isaac Newton’s Second Law of Motion. In other words, this law relates the kinematics of an object to the forces applied to it, and in equation form that relationship looks like this: Force = [Mass] x [Acceleration] “Mass” is the weight of the object, in pounds, divided by the acceleration of the Earth’s gravity. On Earth, the acceleration of gravity is considered to be a constant and is taken to be 32.2 feet per second, per second. (No, that’s not a typo.) Legend has it that Newton discovered the earth’s acceleration when gravity caused an apple to fall from a tree and hit him on the head. That may or may not be true, but Newton’s Second Law of Motion forms the foundation for the study of kinetics. To illustrate how kinetics works, we can look at another very simple example. Suppose you have a block of steel that weighs 50 pounds, and it is sitting still on a nice smooth, frictionless sheet of ice (see Figure 1).
Figure 1
How hard would you have to push on the side of this block to make it accelerate across the ice at a rate of 10 feet per second, per second? Use Newton’s second law to find out: Force = [(50 Lb.) ÷ (32.2 ft./second2)] x [10 ft./second2] Force = 15.5 Lb. Force and energy calculations in kinetics can get really complicated, especially when you have to consider the effects of friction, forces acting at angles, velocity, rotation, motion constraints, collisions, etc. Our next mechanical engineering topic will be: Kinematics of Machines, the study of how parts of machines behave as they move through their ranges of motion. _________________________________________________________________
|
Mechanical Engineering, Focus on Dynamics – Part I, Kinematics
Sunday, October 25th, 2009|
Last week we talked about one of the ten core disciplines of mechanical engineering, statics. Today our focus will shift to a discussion of how mechanical engineers use the study of Dynamics to solve problems. As its name implies, Dynamics involves the study of how things change, or more specifically, how they move. Dynamics can be broken down into two basic parts: kinematics and kinetics. We’ll focus on kinematics this week. Kinematics is the study of the geometry of motion. Kinematics is used to develop a relationship between how far an object travels in a given time, its velocity, and its acceleration. The precipitating cause of the motion is not considered in kinematics. Before beginning our discussion of kinematics, let’s go back to the good ol’ days and revisit what should be some very familiar ground to anyone who’s taken algebra. Does this word problem sound familiar to you: If you start at point X and you’re going at Y speed for a given length of time, T, what distance will you have traveled? Here’s the same problem presented in another way. Suppose you’re driving and you set your cruise control at 70 miles per hour. Out of curiosity you want to know how far your automobile will travel in 15 minutes (0.25 hours). Kinematics teaches that the relationship between velocity, time, and distance can be demonstrated by this equation: Distance = (Velocity) x (Travel Time) Distance = (70 miles/hour) x (0.25 hour) = 17.5 miles Of course kinematics can get far more complicated than this simple example, especially when objects accelerate, decelerate, change direction, and move in paths that are nonlinear, that is, not in a straight line. Next week we’ll talk about the study of kinetics, particularly Sir Isaac Newton’s Second Law of Motion. _________________________________________________________________
|
