|
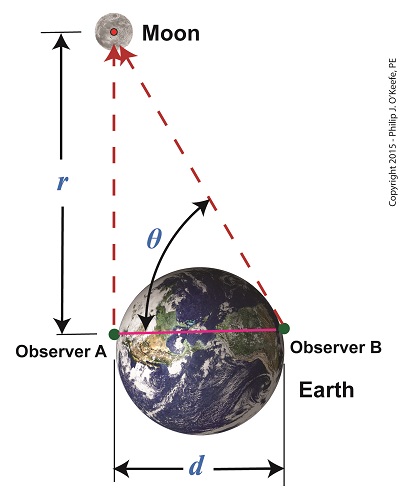
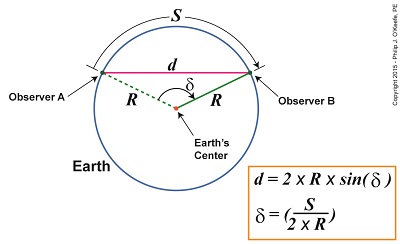
Last time we learned that early scientists used Earth as a huge optical rangefinder to gauge the distance, r, between it and the moon. But before they could put to use our by now very familiar distance calculating formula they needed to first determine the distance, d, between their observation positions. This distance is known within mathematical circles as a chord and is represented by the pink solid line in Figures 1 and 2. A chord is simply a straight line drawn between any two points on a circle, in this case the distance, d, between our observers of the moon. Its length can be determined mathematically if the Earth’s radius, R, and the curved distance, S, between Observers A and B are known. Calculating d was done with relative ease by putting Earth’s circular geometry and principles of mathematics to use. The formula that will accomplish this is shown in Figure 2’s inset box. And here’s the distance calculating formula, yet again: r = d × tan(θ) Figure 2 You will note that Figure 2 features a new symbol, δ , which represents a new angle, and a new trigonometric term, sin( ), or sine. To understand how the angle δ is formed, imagine a green line of length R that extends from Earth’s center to its surface. This is Earth’s radius, as determined by Eratosthenes. The end attached to Earth’s center pivots to allow R‘s other end to travel along Earth’s surface. It travels a path between Observers A and B, represented by curved line S. The angle δ is formed between the dashed green line, which represents R‘s starting point, and R‘s solid green line, which represents its finishing point at Observer B’s location. Figure 2 shows that the angle δ is calculated by dividing S by 2 × R . This numerical value is then entered into a scientific calculator, and when we press the sin button we’re provided with the sine value for angle δ. It should be noted that this is measured in radians, a measuring system typically associated with circles (rather than the more familiar degrees), in order to obtain the correct answer for d. Scientific calculators easily switch between the two modes. Follow this link if you’d like to learn more about radians. Now the Earth is relatively close to the moon, a mere 238,900 miles, and using it as an optical rangefinder to gauge distance to the moon is relatively straightforward. But can it be used to judge the distance to its sun, a whopping 93,000,000 miles away? We’ll see next time why it can’t and what alternate method must be used.
____________________________________
|
Posts Tagged ‘Eratosthenes’
Determining Chord Length on Circle Earth
Tuesday, April 28th, 2015What is Earth’s Mass?
Friday, November 7th, 2014|
Last time we learned how Henry Cavendish used Christiaan Huygens’ work with pendulums to determine the value of g, the acceleration of gravity factor for Earth, to be 32.3 ft/sec2, or 9.8 m/sec2. From there Cavendish was able to go on and arrive at values for other factors in Isaac Newton’s gravity formula, namely G, the universal gravitational constant, and M, Earth’s mass. Today, we’ll discuss how Cavendish was able to calculate the Earth’s mass. Newton’s formula for gravity, once again, is: M = (g × R2) ÷ G where M stands for the mass of the heavenly body being quantified. For our case today M will represent the mass of Earth, which was originally quantified in slugs, a British unit of measurement. Today the measurement unit of choice in most parts of the world is the kilogram, which is the metric equivalent of a slug. With regard to the other variables in Newton’s gravity formula, namely, R and G, their values had previously been determined. Eratosthenes’ measurement of shadows cast by the sun on Earth’s surface had revealed Earth’s radius, R, to be 6,371 kilometers, or 6,371,000 meters. And Cavendish’s experiments led him to conclude that the universal gravitational constant, G, was 6.67 × 10-11 cubic meters per kilogram-second squared. Plugging these values into Newton’s equation, we calculate Earth’s mass to be: M = ((9.8 m/sec2) × (6,371,000 m)2) ÷ (6.67 × 10-11 m3/kg-sec2) M = 5.96 × 1024 kilograms Incidentally, 5.96 × 1024 is scientific notation, or mathematical shorthand, for the number 5,960,000,000,000,000,000,000,000. That’s a whole lot of zeros! Calculating the mass of Earth was an impressive accomplishment. Now that its value was known, scientists would be able to calculate the mass and acceleration of gravity for any heavenly body in the universe. We’ll see how that’s done next time.
_______________________________________
|
How Big is the Earth?
Wednesday, October 8th, 2014|
Last time we discussed Isaac Newton’s Law of Gravitation and how he used it to arrive at conclusions concerning gravity. He theorized the existence of a universal gravitational constant, G, a set numerical value for all heavenly bodies in our universe, and he developed a formula to determine the acceleration of gravity, g. Newton felt sure that the gravity at play on the surface of any heavenly body, such as stars and planets, could be determined if one knew the value of G, along with the object’s mass, M, and radius, R, and he developed this equation to do so, g = (G × M) ÷ R2 At this point you may be thinking, Finding the mass and radius of a heavenly body is hard enough, but what is this universal gravitational constant?? Good point. Back in Newton’s time, the existence of G was purely speculative. He conceived it to be a numerical value which would act as a fudge factor, enabling his equation for determining g to work. As a matter of fact, Newton had no clue of how to determine G and was convinced that it would be beyond anyone’s ability to do so. The mysterious G factor and its numerical value were not actually determined until more than a hundred years later by Henry Cavendish. In 1796 Cavendish was focused on determining the Earth’s mass, M, by using Newton’s equation. To arrive at a value for G, Cavendish conducted experiments which measured the gravitational attraction between two lead spheres attached by way of a torsion balance. After much testing he eventually concluded that he had computed G to a reasonable degree of accuracy and that its value was equal to 3.439 x 10-8 cubic feet per slug per second squared. In this case a slug is not a slimy creature living in the garden, but rather a unit of measurement used to quantify the mass of an object. For the full story, see this article on Cavendish’s experiment by The Physics Classroom. But even after determining G, Cavendish still had to obtain values for g and R in order to calculate M. This was made possible thanks to the work of two men who came before him. One of these was the Greek mathematician Eratosthenes, who way back in 230 B.C. discovered that the radius of the earth, R, could be calculated by simply measuring the shadows of objects cast on Earth’s surface. All he needed was a measuring stick and geometry. For the full story see this fascinating article on the subject from Bucknell University. As for the value of g, the acceleration of gravity on Earth, Cavendish was aided by the previous efforts of a Dutch mathematician from Newton’s time, Christiaan Huygens. You may recall that Huygens was first introduced in a previous blog series on spur gear geometry, where we learned that he studied the motion of clock pendulums. Through observation, Huygens was able to arrive at a mathematical formula capable of predicting the pendulums’ often erratic motion on ships at sea. Next time we’ll see how Huygens’ insights gained by watching pendulums ultimately made it possible for him to arrive at a numerical value for Earth’s acceleration of gravity, g. _______________________________________
|