|
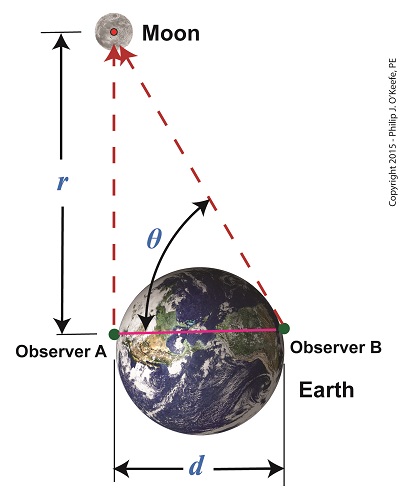
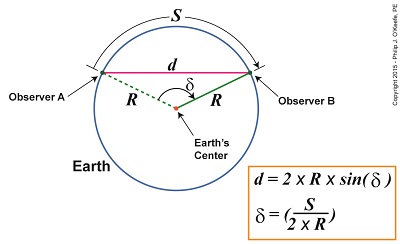
Last time we learned that early scientists used Earth as a huge optical rangefinder to gauge the distance, r, between it and the moon. But before they could put to use our by now very familiar distance calculating formula they needed to first determine the distance, d, between their observation positions. This distance is known within mathematical circles as a chord and is represented by the pink solid line in Figures 1 and 2. A chord is simply a straight line drawn between any two points on a circle, in this case the distance, d, between our observers of the moon. Its length can be determined mathematically if the Earth’s radius, R, and the curved distance, S, between Observers A and B are known. Calculating d was done with relative ease by putting Earth’s circular geometry and principles of mathematics to use. The formula that will accomplish this is shown in Figure 2’s inset box. And here’s the distance calculating formula, yet again: r = d × tan(θ) Figure 2 You will note that Figure 2 features a new symbol, δ , which represents a new angle, and a new trigonometric term, sin( ), or sine. To understand how the angle δ is formed, imagine a green line of length R that extends from Earth’s center to its surface. This is Earth’s radius, as determined by Eratosthenes. The end attached to Earth’s center pivots to allow R‘s other end to travel along Earth’s surface. It travels a path between Observers A and B, represented by curved line S. The angle δ is formed between the dashed green line, which represents R‘s starting point, and R‘s solid green line, which represents its finishing point at Observer B’s location. Figure 2 shows that the angle δ is calculated by dividing S by 2 × R . This numerical value is then entered into a scientific calculator, and when we press the sin button we’re provided with the sine value for angle δ. It should be noted that this is measured in radians, a measuring system typically associated with circles (rather than the more familiar degrees), in order to obtain the correct answer for d. Scientific calculators easily switch between the two modes. Follow this link if you’d like to learn more about radians. Now the Earth is relatively close to the moon, a mere 238,900 miles, and using it as an optical rangefinder to gauge distance to the moon is relatively straightforward. But can it be used to judge the distance to its sun, a whopping 93,000,000 miles away? We’ll see next time why it can’t and what alternate method must be used.
____________________________________
|
Engineering Expert Witness Blog
Published by Philip J. O'Keefe, PE, MLE