|
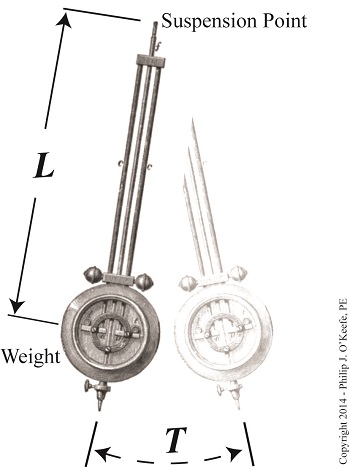
What would you do to pass the time if you were stuck on a ship of the middle ages for weeks at a time? Dutch mathematician Christiaan Huygens used the time to study the movement of clock pendulums. He watched them for endless hours, and he eventually came to realize that the pendulums’ swing was uneven due to the ship’s listing on the waves, a phenomenon which also affected the ship’s clocks’ accuracy. Eager to devise a solution to the problem of inaccurate time keeping, Huygens dedicated himself to finding a solution to the problem, and in so doing increase the navigational accuracy of ships as well. His efforts eventually resulted in a formula that shared a common variable with Isaac Newton’s gravitational formula, namely, g, Earth’s acceleration of gravity factor, a value which Huygens posited was indeed a non varying constant. Building upon Newton’s work, Huygens devised a formula which demonstrated the mathematical relationship between the motion of a clock’s pendulum and g. That formula is, T = 2 × ∏ × (L ÷ g)1/2 where, T is the period of time it takes a pendulum to make one complete swing, ∏ the Greek symbol pi, valued at 3.14, and L the length of the pendulum. Since devices capable of directly measuring the Earth’s gravity did not exist then, as they still don’t exist today, how in the world (pardon the pun) was Huygens able to arrive at this formula? Thinking outside the box, he posited that if one knows the length of the pendulum L, and then accurately measures the time it takes for the pendulum to complete its swings, taking into account the varied times that resulted due to the ship’s listing, one can calculate g using his equation. He eventually determined g‘s value to be equal to 32.2 feet per second per second, or 32.2 ft/sec2. Fast forwarding to Henry Cavendish’s time, Huygens’ work with pendulums and his determination of g was well known. We’ll see what Cavendish did with this knowledge next time.
_______________________________________
|
Posts Tagged ‘ship navigation’
How Long is a Pendulum’s Swing?
Wednesday, October 29th, 2014Tags: acceleration of gravity, Christiaan Huygens, Earth's gravity, engineering expert witness, falling objects, forensic engineer, gravity, Isaac Newton, Newton's gravitational formula, pendulum, period of swing, ship navigation
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | Comments Off on How Long is a Pendulum’s Swing?