|
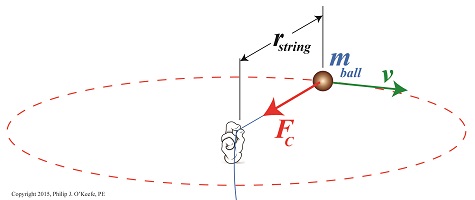
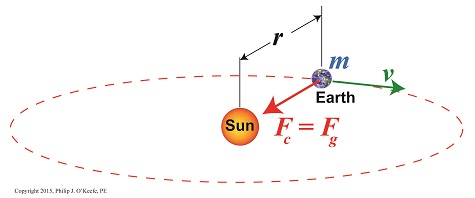
Last time we saw how centripetal force is responsible for keeping a child’s ball moving in a circular path when twirled above his head. Today we’ll see how that same force is responsible for keeping Earth in its rotation around the sun. We’ll use Isaac Newton’s Second Law of Motion as it relates to centripetal force to bear that out today. Our example from last week, Figure 1 According to Newton’s Second Law of Motion, Fc, the centripetal force acting upon the ball, is calculated by the equation, Fc = [mball × v2] ÷ rstring where, mball is the ball’s mass, v the ball’s velocity, and rstring is the length of the string. The mechanics are obviously different with regard to Earth and its orbit around the sun, where there’s no obvious physical link between the objects in rotation. In this case the sun’s gravitational force, Fg, acts to tether Earth to it. And just like the string and ball, the sun’s gravitational tether creates a centripetal force, Fc, which prevents Earth from leaving its orbital path. See Figure 2. Figure 2 Newton concluded that for the Earth to remain on its permanent, fixed path of orbit around the sun, Fc must be equal to Fg, and that the forces in play between the sun and Earth were like a gigantic tug of war where neither side is able to pull any harder than the other. This stalemate is responsible for keeping Earth stably in place in its orbit. According to Newton’s Second Law, the sun’s gravitational force acting upon the Earth is calculated by, Fg = Fc = [m × v2] ÷ r where, m is Earth’s mass, v its orbital velocity, and r the distance between Earth and the sun. Thanks to early scientists like Edmund Halley and Henry Cavendish, the values for m and r had already been determined. That left v, Earth’s orbital velocity, the only variable remaining to be solved. We’ll see how 19th Century scientists accomplished that next time.
____________________________________
|
Posts Tagged ‘centripetal force’
Centripetal Force Makes the Earth Go Round
Thursday, July 9th, 2015Centripetal Force
Friday, July 3rd, 2015|
Have you ever wondered how Earth keeps its steady orbit around its life sustaining sun, or what prevents it from breaking away and flying off willy-nilly into the universe? It’s more than just simple gravity, it’s the physics behind centripetal force, the topic we’ll be exploring today. We’ve been working our way towards a full discussion on gravity in this long blog series, navigating subjects such as the behavior of falling objects, the acceleration of gravity, the masses of Earth and the sun, and the optical measurement of cosmic distances. We’ve now come full circle from my opening blog on the subject, Gravity and the Mass of the Sun. In that blog an equation was introduced as a means to calculate the mass of the sun, and in that equation is the variable we’ll be working towards solving today, Fg, the sun’s gravitational force upon the Earth. Here again is that equation, M = (Fg × r2) ÷ (m × G) Gravity, mass, and distance all come into play in forming the structure of our universe, and the variables in this equation reflect that: M, the mass of the sun, r the distance between Earth and the sun, m the Earth’s mass, and G the universal gravitational constant. With the exception of Fg, all variables in this equation have already been solved for in previous blogs in this series. For a refresher go to, Calculating the Distance to the Sun, What is Earth’s Mass? and Newton’s Law of Gravitation and the Universal Gravitational Constant. As there is no direct means to measure the cosmic quantity, Fg, we’re left to an indirect method for its computation. The indirect method is based on the phenomenon of centripetal force, Fc something most children become acquainted with when they experience the thrill of twirling an object attached to a string, say a rubber ball, above their heads. See Figure 1. Figure 1 As the ball is twirled, the string becomes taut. The energy exerted upon it by the child’s hand, coupled with the ball’s mass and traveling speed/velocity, v, make the ball want to move off in a straight trajectory into space, like a launched projectile. But the string it’s attached to prevents it from doing so, forcing the ball to instead travel a circular path around the center point of rotation. The taut string and the ball’s circular path are evidence of centripetal force, Fc, at work. Next time we’ll employ Isaac Newton’s Second Law of Motion to the centripetal force phenomenon to see how the sun’s gravitational force keeps Earth in a stable circular orbit around the sun.
____________________________________
|