|
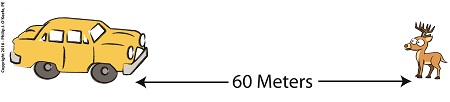
I’m sometimes called upon to render an engineering expert opinion on auto accidents, and in our last blog we stretched this application to a scenario in which Santa’s sleigh collided with the opposing force of a strong wind. At that time we used the Work-Energy Theorem to calculate the amount of food energy Rudolph and his team required to regain speed and get back on schedule. Today we’ll use the Theorem to analyze the forces at play in another deer scenario and calculate the braking distance a car needs to avoid hitting one on the highway. The average sedan has a mass of about 1,500 pounds, or 680 kilograms. In our example it’s driving down the highway at a speed, or velocity, of 30 miles per hour, which equates to it covering a distance of 13.3 meters, or just under 44 feet, per second. A deer jumps onto the highway, 60 meters in front of the car. The alert driver slams on the brakes, which exert 1200 Newtons of stopping force on the car. If you’ll recall from past blogs in this series, the Newton is the metric unit used to measure force.
Did Bambi survive? Let’s use the Work-Energy Theorem to find out. Here it is again, F × d = ½ × m × [v22 – v12] where, F is the braking force used to slow a car of mass m, from an initial velocity of v1 to a final velocity of v2 in a braking distance, d. The car will eventually come to a complete stop as the driver attempts to avoid hitting the deer, so its final velocity, v2, will be zero. The Work-Energy Theorem is most often stated in terms of metric units, the measuring unit of choice in the scientific community, and we’ll follow suit with our math. Inserting these values into the equation, we get, [1200 Newtons] × d = ½ × [680 kilograms] × [(0)2 – (13.3 meters per second)2] Using algebra to solve for d, the braking distance, we arrive at, d = ½ × [680 kilograms] × [(0)2 – (13.3 meters per second)2] ÷ [1200 Newtons] d = 50.11 meters The car stopped 50.11 meters from the point when the driver slammed on his brakes, just about 10 meters short of hitting the deer. Bambi lives to leap another day! Next time we’ll use the Work-Energy Theorem to assess the fate of the falling coffee mug we introduced in past blogs when we opened our discussion on the different forms of energy.
Copyright 2016 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |