|
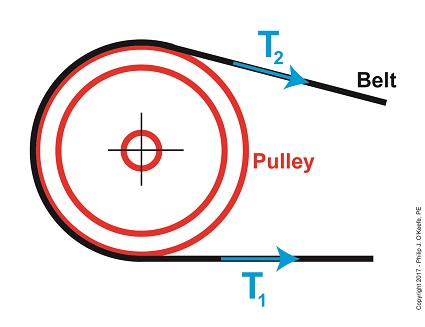
Last time we introduced some of the variables in the Euler-Eytelwein Formula, an equation used to examine the amount of friction present in pulley-belt assemblies. Today we’ll explore its two tension-denoting variables, T1 and T2. Here again is the Euler-Eytelwin Formula,where, T1 and T2 are belt tensions on either side of a pulley, T1 = T2 × e(μθ) T1 is known as the tight side tension of the assembly because, as its name implies, the side of the belt containing this tension is tight, and that is so due to its role in transmitting mechanical power between the driving and driven pulleys. T2 is the loose side tension because on its side of the pulley no mechanical power is transmitted, therefore it’s slack–it’s just going along for the ride between the driving and driven pulleys. Due to these different roles, the tension in T1 is greater than it is in T2. The Two T’s of the Euler-Eytelwein Formula In the illustration above, tension forces T1 and T2 are shown moving in the same direction, because the force that keeps the belt taught around the pulley moves outward and away from the center of the pulley. According to the Euler-Eytelwein Formula, T1 is equal to a combination of factors: tension T2 ; the friction that exists between the belt and pulley, denoted as μ; and how much of the belt is in contact with the pulley, namely θ. We’ll get into those remaining variables next time. Copyright 2017 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |
Tags: belt, belt tension, driven pulley, driving pulley, engineering, Euler-Eytelwein Formula, mechanical power transmission, pulley