Engineering Expert Witness Blog

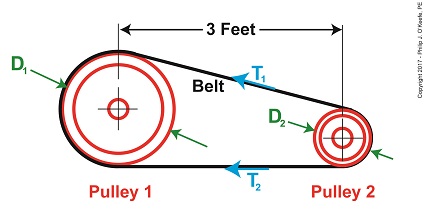
   Sometimes things which appear simple turn out to be rather complex.   Such is the case with the Euler-Eytelwein Formula, a small formula with a big job.   It computes how friction, an omnipresent phenomenon in mechanical assemblies, contributes to the transmission of mechanical power.   Today we’ll determine the value of one of the Euler-Eytelwein Formula’s variables, the angle of wrap.

Determining Angle of Wrap

   Here again is the basis for our calculations, the Euler-Eytelwein Formula.

T₁ = T_{2 ×} e^(μθ)                                                                 (1)

   To recap what we’ve discussed thus far, T₁ is the tight side tension, the maximum the belt can endure before breaking.   T₂ is the loose side tension.   It’s just going along for the ride.   The term e is Euler’s Number, a constant equal to 2.718, and the coefficient of friction, μ, for contact points between the belt and pulleys is 0.3 based on their materials.

   The formula introduced last time to calculate the angle of wrap, θ, is,

θ = (180 – 2α) × (π  ÷ 180)                                             (2)

where,

α = sin^-1((D₁ – D₂) ÷ 2x)                                                 (3)

   By direct measurement we’ve determined the pulleys’ diameters, D₁ and D₂, are equal to 1 foot and 0.25 feet respectively.   The term x is the distance between the two pulley shafts, 3 feet.   The term sin^-1 is a trigonometric function known as inverse sine, a button commonly found on scientific calculators.

   Inserting our known values into equation (3) we arrive at,

α = sin^-1((1.0 foot – 0.25 feet) ÷ 2 × (3 feet))                  (4)

α = 7.18                                                                        (5)

   We can now incorporate equation (5) into equation (2) to solve for θ,

θ = (180 – (2 × 7.18)) × (π ÷ 180)                                  (6)

θ = 2.89                                                                         (7)

   Inserting the values for m and θ into equation (1) we arrive at,

T₁ = T₂ × 2.718^{(0.3 × 2.89)}                                               (8)

T₁ = 2.38T₂                                                                    (9)

   We have at this point solved for over half of the unknown variables in the Euler-Eytelwein Formula.   We still can’t solve for T₁, because we don’t know the value of T₂.   But that will change next time when we introduce yet another formula, this one to determine the amount of mechanical power present in our pulley-belt system.

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________