Posts Tagged ‘mechanical power’

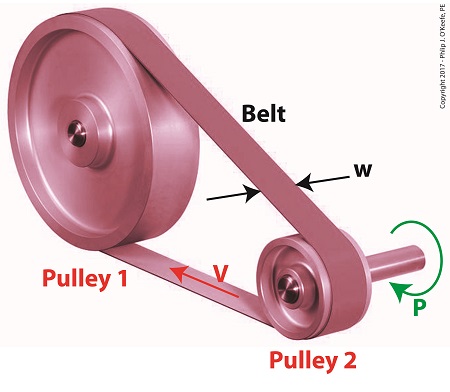
Optimizing Belt Width in a Pulley-Belt Assembly

Friday, September 15th, 2017

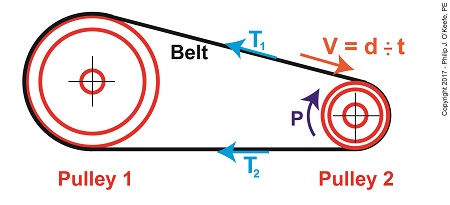
   It’s been awhile since we began our discussion of a pulley-belt assembly operating within a hydroponics plant, and we’ve solved for a lot variables and derived many equations along the way.   Today we’ll tackle the two remaining variables,  T1 , the belt’s tight side tension, and T2 , its loose side tension, and we’ll determine exactly what belt width will optimize power transmission within our system.

 Optimizing Belt Width in a Pulley-Belt Assembly

Optimizing Belt Width in a Pulley-Belt Assembly

   

   Last time we converted mechanical power, P, from horsepower into foot-pounds per second and the belt’s velocity, V, into feet per second in order to get things into terms we can work with.   We then inserted these values into the mechanical power formula to get,

2,200 foot pounds per second = (T1 – T2) × 3.93 feet/second               (1)

   This equation will allow us to solve for T1 and T2, and from there we’ll develop a value for the optimum belt width.

   Previously, we determined from the Euler-Eytelwein Formula that,

T1 = 2.38T2                                                                                     (2)

   Substituting equation (2) into equation (1), we get,

2,200 foot pounds per second = (2.38T2  – T2) × 3.93 feet/second      (3)

   Reducing this equation with algebra we arrive at,

T2 = 405.65 pounds                                                                         (4)

   We can now insert equation (4) into equation (2) and calculate T1,

T1 = 2.38 × 405.65 pounds                                                               (5)

T1 = 965.44 pounds                                                                         (6)

 

   T1 is maximum tension in the belt, specified by the manufacturer to be 300 pounds per inch of width, which makes the minimum width belt to be used to optimize power transmission within our  pulley-belt assembly,

w = T1 ÷ 300 pounds per inch                                                           (7)

w = 965.44 pounds ÷ 300 pounds per inch                                         (8)

w = 3.22 inches                                                                                (9)

   We can use a belt of minimum width of 3.22 inches to safely transmit 4 horsepower from the engine to the pump without incurring breakage and slippage along the belt, thereby optimizing power transmission within our assembly.   If we used a narrower belt, breaking and slippage would occur.   If we used a wider belt, an unnecessary expense would be incurred.

   Next time we’ll begin a discussion on flywheels as they apply to rotating machinery like gasoline and steam engines.

 

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Optimizing Belt Width in a Pulley-Belt Assembly

Unit Conversion, Horsepower to Foot-Pounds per Second

Monday, September 4th, 2017

   We’ve been working our way towards developing values for variables in our example pulley-belt assembly, and last time we calculated the velocity of the belt in that assembly to be 237.99 feet per minute.   But before we can go on to calculate the belt’s loose side tension, T2, and tight side tension, T1, we’ll need to discuss unit conversion, specifically how to convert horsepower into foot-pounds per second.

   Our working formula for this demonstration is the formula for mechanical power, P, previously introduced and shown again here,

P = (T1 – T2) × V                                                               (1)

   By engineering convention mechanical power is normally measured in units of foot-pounds per second.   But if you’ll recall from a past blog in which we determined the belt’s velocity, V, it was measured in units of feet per minute, not per second. 

   To further complicate things, the difference in belt tensions, T1 – T2, is stated in units of pounds, and combining these elements together results in P being expressed in foot-pounds per minute, not the required per second, because we are multiplying feet per minute by pounds.   That’s a whole lot of unit changing within a single equation, which makes for an awkward situation.

   To smooth things out we’ll have to do some converting of units.   We’ll start by dividing V by 60 seconds per minute so it can be expressed in units of feet per second,

V = 237.99 feet per minute ÷  60 seconds per minute          (2)

 V = 3.93 feet/second                                                        (3)

   The power in our belt was previously given as 4 horsepower, which must also undergo conversion and be put in terms of foot-pounds per second so it can be used in equation (1).

Unit Conversion, Horsepower into Foot-Pounds

Unit Conversion, Horsepower to Foot-Pounds per Second

   

   One horsepower is equal to 550 foot-pounds per second, which makes the amount of power, P, in our pulley-belt assembly equal to 2,200 foot-pounds per second.

   Units converted, we can now insert the values for V and P into equation (1) to arrive at,

2,200 foot pounds per second = (T1 – T2) × 3.93 feet/second           (4)

   Next time we’ll use this relationship to develop values for T1 and T2, the belt’s tight and loose side tensions.

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Unit Conversion, Horsepower to Foot-Pounds per Second

The Mechanical Power Formula in Pulley and Belt Assemblies

Saturday, July 29th, 2017

     Last time we determined the value for one of the key variables in the Euler-Eytelwein Formula known as the angle of wrap.   To do so we worked with the relationship between the two tensions present in our example pulley-belt assembly, T1 and T2.   Today we’ll use physics to solve for T2 and arrive at the Mechanical Power Formula, which enables us to compute the amount of power present in our pulley and belt assembly, a common engineering task.

    To start things off let’s reintroduce the equation which defines the relationship between our two tensions, the Euler-Eytelwein Formula, with the value for e, Euler’s Number, and its accompanying coefficients, as determined from our last blog,

T1 = 2.38T2                            (1)

    Before we can calculate T1 we must calculate T2.   But before we can do that we need to discuss the concept of power.

 The Mechanical Power Formula in Pulley and Belt Assemblies

 The Mechanical Power Formula in Pulley and Belt Assemblies

   

    Generally speaking, power, P, is equal to work, W, performed per unit of time, t, and can be defined mathematically as,

P = W ÷ t                               (2)

    Now let’s make equation (2) specific to our situation by converting terms into those which apply to a pulley and belt assembly.   As we discussed in a past blog, work is equal to force, F, applied over a distance, d.   Looking at things that way equation (2) becomes,

P = F × d ÷ t                         (3)

    In equation (3) distance divided by time, or “d ÷ t,” equals velocity, V.   Velocity is the distance traveled in a given time period, and this fact is directly applicable to our example, which happens to be measured in units of feet per second.   Using these facts equation (3) becomes,

P = F × V                               (4)

    Equation (4) contains variables that will enable us to determine the amount of mechanical power, P, being transmitted in our pulley and belt assembly.

   The force, F, is what does the work of transmitting mechanical power from the driving pulley, pulley 2, to the passive driven pulley, pulley1.   The belt portion passing through pulley 1 is loose but then tightens as it moves through pulley 2.   The force, F, is the difference between the belt’s tight side tension, T1, and loose side tension, T2.   Which brings us to our next equation, put in terms of these two tensions,

P = (T1 – T2) × V                   (5)

    Equation (5) is known as the Mechanical Power Formula in pulley and belt assemblies.

    The variable V, is the velocity of the belt as it moves across the face of pulley 2, and it’s computed by yet another formula.   We’ll pick up with that issue next time.

 

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Mechanical Power Formula in Pulley and Belt Assemblies

Determining Angle of Wrap

Monday, July 17th, 2017

   Sometimes things which appear simple turn out to be rather complex.   Such is the case with the Euler-Eytelwein Formula, a small formula with a big job.   It computes how friction, an omnipresent phenomenon in mechanical assemblies, contributes to the transmission of mechanical power.   Today we’ll determine the value of one of the Euler-Eytelwein Formula’s variables, the angle of wrap.

Determining Angle of Wrap

Determining Angle of Wrap

   Here again is the basis for our calculations, the Euler-Eytelwein Formula.

T1 = T2 × e(μθ)                                                                 (1)

   To recap what we’ve discussed thus far, T1 is the tight side tension, the maximum the belt can endure before breaking.   T2 is the loose side tension.   It’s just going along for the ride.   The term e is Euler’s Number, a constant equal to 2.718, and the coefficient of friction, μ, for contact points between the belt and pulleys is 0.3 based on their materials.

   The formula introduced last time to calculate the angle of wrap, θ, is,

θ = (180 – 2α) × (π  ÷ 180)                                             (2)

where,

α = sin-1((D1 – D2) ÷ 2x)                                                 (3)

   By direct measurement we’ve determined the pulleys’ diameters, D1 and D2, are equal to 1 foot and 0.25 feet respectively.   The term x is the distance between the two pulley shafts, 3 feet.   The term sin-1 is a trigonometric function known as inverse sine, a button commonly found on scientific calculators.

   Inserting our known values into equation (3) we arrive at,

α = sin-1((1.0 foot – 0.25 feet) ÷ 2 × (3 feet))                  (4)

α = 7.18                                                                        (5)

   We can now incorporate equation (5) into equation (2) to solve for θ,

θ = (180 – (2 × 7.18)) × (π ÷ 180)                                  (6)

θ = 2.89                                                                         (7)

   Inserting the values for m and θ into equation (1) we arrive at,

T1 = T2 × 2.718(0.3 × 2.89)                                               (8)

T1 = 2.38T2                                                                    (9)

   We have at this point solved for over half of the unknown variables in the Euler-Eytelwein Formula.   We still can’t solve for T1, because we don’t know the value of T2.   But that will change next time when we introduce yet another formula, this one to determine the amount of mechanical power present in our pulley-belt system.

 

 

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Determining Angle of Wrap

The Difference Between Driven and Driving Pulleys

Friday, March 31st, 2017

    Last time we introduced two historical legends in the field of engineering who pioneered the science of mechanical power transmission using belts and pulleys, Leonhard Euler and Johann Albert Eytelwein.   Today we’ll build a foundation for understanding their famous Euler-Eytelwein Formula through our example of a simple mechanical power transmission system consisting of two pulleys and a belt, and in so doing demonstrate the difference between driven and driving pulleys.

    Our example of a basic mechanical power transmission system consists of two pulleys connected by a drive belt.   The driving pulley is attached to a source of mechanical power, for example, the shaft of an electric motor.   The driven pulley, which is attached to the shaft of a piece of rotating machinery, receives the mechanical power from the electric motor so the machinery can perform its function.

The Difference Between Driven and Driving Pulleys

The Difference Between Driven and Driving Pulleys 

   

    Next time we’ll see how driven pulleys can be made to spin at different speeds from the driving pulley, enabling different modes of operation in mechanical devices.

Copyright 2017 – Philip J. O’Keefe, PE

Engineering Expert Witness Blog

____________________________________

 

Tags: , , , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on The Difference Between Driven and Driving Pulleys

The Relationship Between Torque and Horsepower

Tuesday, July 15th, 2014
      We’ve been discussing gear trains for some time now, and last time we posed the question:  Why even bother using a gear train and performing complex computations to arrive at a desired torque for an application?   Why not just use a bigger motor to start with?   Today we’ll see why.

      First, we must acknowledge that sometimes higher torque is achieved by simply using a more powerful motor.   But sometimes this isn’t possible or practical.

      To begin our discussion, we must first understand how torque is related to motor power, the amount of mechanical work a motor can perform.   Torque is in fact a function of how much mechanical power a motor produces.   In the United States motor power is typically measured in units of horsepower.

      The following equation illustrates the relationship between torque, horsepower, and motor speed:

T = [HP ÷  n]  ×  63,025

where T is the motor shaft’s torque in units of inch-pounds, HP is the motor’s horsepower, and n is the speed of the motor shaft in revolutions per minute (RPM).   The number 63,025 in the equation is a constant used to convert the units of horsepower and RPM into units of torque (inch pounds).   This equation applies to all sources of mechanical power.   Its versatility enables design engineers to easily determine if a mechanical power source can deliver the torque required to drive a particular piece of machinery.

      The torque equation above tells us that in order to get a higher torque T for a given speed n, you’ll have to get a motor with a higher HP.   Put another way, if your speed remains constant and you use a motor with higher horsepower, you’ll get more torque for your application simply by increasing the horsepower.

      Next time we’ll plug numbers into our equation and see how it all works.

_______________________________________

Tags: , , , , , , , , , ,
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability, Professional Malpractice | Comments Off on The Relationship Between Torque and Horsepower