|
Last time we introduced the Mechanical Power Formula, which is used to compute power in pulley-belt assemblies, and we got as far as introducing the term tangential velocity, V, a key variable within the Formula. Today we’ll devise a new formula to compute this tangential velocity. Our starting point is the formula introduced last week to compute the amount of power, P, in our pulley-belt example is, again, P = (T1 – T2) × V (1) We already know that P is equal to 4 horsepower, we have yet to determine the belt’s tight side tension, T1, and loose side tension, T2, and of course V, the formula for which we’ll develop today.
Tangential Velocity
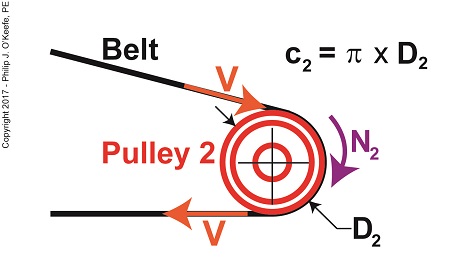
Tangential velocity is dependent on both the circumference, c2, and rotational speed, N2, of Pulley 2. The circumference represents the length of Pulley 2’s curved surface. The belt travels part of this distance as it makes its way from Pulley 2 back to Pulley 1. The rotational speed, N2, represents the rate that it takes for Pulley 2’s curved surface to make one revolution while propelling the belt. This time period is known as the period of revolution, t2, and is related to N2 by this equation, N2 = 1 ÷ t2 (2) The rotational speed of Pulley 2 is specified in our example as 300 RPMs, or revolutions per minute, and we’ll denote that speed as N2 in light of the fact it’s referring to speed present at the location of Pulley 2. As we build the formula, we’ll be converting N2 into velocity, specifically tangential velocity, V, which is the velocity at which the belt operates, this in turn will enable us to solve equation (1). Why speak in terms of tangential velocity rather than plain old ordinary velocity? Because the moving belt’s orientation to the surface of the pulley lies at a tangent in relation to the pulley’s circumference, c2, as shown in the above illustration. Put another way, the belt enters and leaves the curved surface of the pulley in a straight line. Generally speaking, velocity is distance traveled over a period of time, and tangential velocity is no different. So taking time into account we arrive at this formula, V = c2 ÷ t2 (3) Since the surface of Pulley 2 is a circle, its circumference can be computed using a formula developed thousands of years ago by the Greek engineer and mathematician Archimedes. It is, c2 = π × D2 (4) where D2 is the diameter of the pulley and π represents the constant 3.1416. We now arrive at the formula for tangential velocity by combining equations (3) and (4), V = π × D2 ÷ t2 (5) Next time we’ll plug numbers into equation (5) and solve for V. Copyright 2017 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |
Tags: belt, belt velocity, circumference, engineer, loose side tension, mechanical power formula, period of revolution, pulley, pulleys, speed, tangential velocity, tight side tension, velocity