|
Last week we talked about psychrometry, which involves the analysis of gas and vapor mixtures like air and water. This week we’ll begin our discussion of fluid mechanics, which is the study of the force, pressure, and energy on both stationary and moving fluids. We’ll focus on stationary fluids this week. Let’s clear one thing up before we go any further. By “fluid,” I mean a substance that deforms continuously under a shearing stress, no matter how small. That means that when you try to cut it with a knife, a fluid just gives way under the knife and comes back together again after the knife passes through it. Remember the T-1000 liquid metal man in the movie Terminator II? Now that’s what I’m talking about! Now we all know that liquids are fluids, but did you know that gases are, too? An important concept in fluid mechanics is that liquids, like water and oil, cannot be compressed much when you push down on them in an enclosed container. This is because the molecules of liquids are tightly packed together and they can’t squeeze together any tighter. So, liquids are considered to be incompressible fluids. On the other hand, when you push down on a gas, take air for example, you can compress it within the container. This is because the gas molecules are far apart from each other, so there is plenty of room for them to come closer together. Since there is so much room between their molecules, gases are considered to be compressible fluids. Let’s begin our exploration of fluid mechanics by examining fluids that don’t move, meaning they are static. This field is also known as the study of fluid statics, otherwise known as hydrostatics. We’ll talk about fluids that move, that is, fluid dynamics, later in our series. To show how fluid statics works, suppose you have a hydraulic bottle jack in your garage like the one in Figure 1. When you push down on the lever, it doesn’t take a whole lot of muscle to lift something heavy like a car. Why is that? Let’s see how the jack works by looking at a cutaway diagram. See Figure 2.
Figure 1 – A Hydraulic Bottle Jack Used To Lift A Car
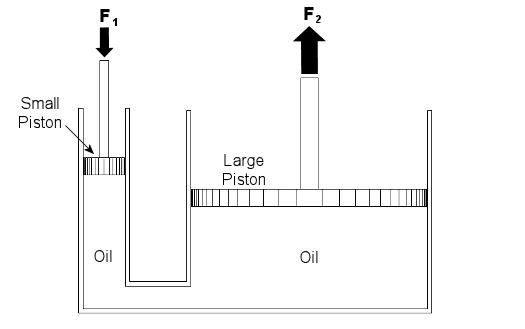
Figure 2 – Inside a Hydraulic Bottle Jack
The jack basically consists of two cylinders, one small, one large. The two cylinders are each filled with oil, and there is a passage between them. Inside each cylinder is a piston. The oil in the jack is a liquid, so it’s incompressible. When you push down on the jack’s lever, you create a force, F1, on the small piston. This then creates equal pressure in the oil under both the small and large pistons. Why? Because the liquid molecules are so tightly packed together, they push against each other and pressure is transmitted equally on all surfaces inside the jack. Now “pressure” is simply a force divided by a unit of area, for example, pounds of force per square inch. In our example it’s the large piston that’s going to lift the weight of the car. Because the large piston has a much larger surface area than the small piston, the fluid in the large cylinder will create a much larger force, F2, to bear up against the car’s weight, thereby lifting it off the ground. Now suppose the small piston has a surface area of 2 square inches, the large piston has a surface area of 20 square inches, and F1 is equal to 50 pounds of force. Since the oil pressure is equal under both pistons as stated above, we can write the flowing equation: Oil Pressure in the Small Piston = Oil Pressure in the Large Piston Once again, pressure is force divided by area, so for our hydraulic jack we can rewrite the equation as follows: (F1)/(Area of the Small Piston) = (F2)/(Area of the Large Piston) Okay, we’re in good shape here, because we know three things: F1, the area of the small piston, and the area of the large piston. So, by plugging this information into the equation, we can use algebra to solve for the upward force, F2, required to lift the car: (50lbf)/(2in2) = (F2)/(20in2) F2 = [(50lbf)/(2in2)] x (20in2) F2 = 500lbf = 500 Pounds of Force So what’s happened here? Well, like magic, the jack uses fluid statics to multiply the input force by a factor of ten. When you push down on the jack handle with 50 pounds of force, you actually produce 500 pounds of force, enough to lift the car. If you made the large piston wider, then its area would be much greater still. For example, if we doubled the size of the large piston from 20 square inches to 40 square inches, F2 would be doubled, so you’d end up with 1000 pounds of force, more than enough to lift an oversized vehicle, like an SUV. Miraculously, the force used to push down on the small piston would remain the same, so there’s no need to worry if you’re a 100-pound weakling. Next week we’ll continue with Part II of our discussion of Fluid Mechanics and talk further about fluid statics.
_________________________________________________________________
|
Engineering Expert Witness Blog
Published by Philip J. O'Keefe, PE, MLE