|
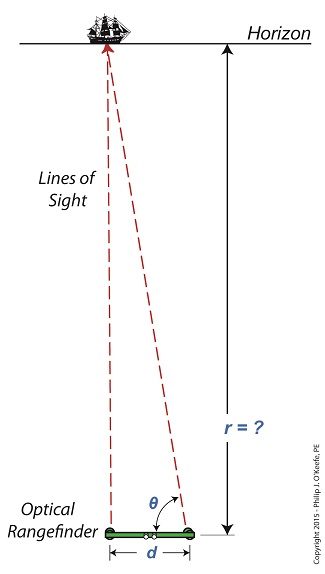
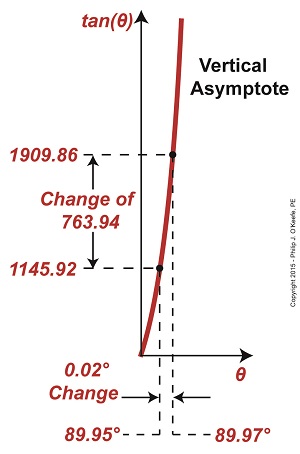
Last time we touched on the limitations of optical rangefinders when attempting to measure extremely long distances. Today we’ll expand on that theme. Let’s say we want to use a rangefinder to determine the distance, r, to an object that’s extremely far away, like a ship on a distant horizon, as shown in Figure 1. Figure 1 It’s obvious that the rangefinder’s length, d, is extremely small in comparison to the total distance viewed, r. When this situation exists, a very long and narrow right triangle is formed between the lines of sight provided by mirrors A and B of the rangefinder, represented by two red dashed lines, and the length of the rangefinder itself, d. It’s still a right triangle, a necessary condition to using our rangefinder formula to determine distance, however, when the triangle is an extremely long, narrow one, the angle θ approaches 90° in value. As discussed in a previous article, a θ value of 90° is impossible for the rangefinder distance formula to work with. The more distant the ship, the longer and narrower the triangle becomes, causing θ to creep ever closer to 90°. From a trigonometric point of view, this spells trouble. The problem is, the closer θ gets to 90°, the greater the disparity potential in its measurement. For example, let’s suppose that when the ship is first sighted with the rangefinder θ is measured at 89.95°. Then a second later the same person seeks to verify his measurement. Without noticing that he’s doing it, he shifts weight on his foot ever so slightly, takes a second reading, and finds that this time θ is 89.97°. That’s a difference of only 0.02° between readings, but it produces a huge change in the tan(θ). Figure 2 represents a graph of these two measurements, with the angle θ values on one axis, the tan(θ) values on the other. Figure 2 The graph illustrates how this minute change in θ of only two hundredths of a degree (0.02°) results in a correspondingly huge change to tan(θ) of 763.94 units. We know that the rangefinder’s length, d, equals 3 feet, so plugging all the numbers into our rangefinder formula we determine the distance to the ship to be, r = d × tan(θ) r = 3 feet × 763.94 = 2291.82 feet What this means on a practical usability level is that when the rangefinder’s adjustable mirror B moves only two one hundredths of a degree, it results in a change to the distance viewed, r, of almost half a mile! There’s another problem that goes hand in hand with the one presented today. We’ll explore it next time.
____________________________________
|
Tags: engineering expert witness, forensic engineer, mechanical engineering expert witness, optical distance measurement, parallax, tangent, trigonometry, vertical asymptote