|
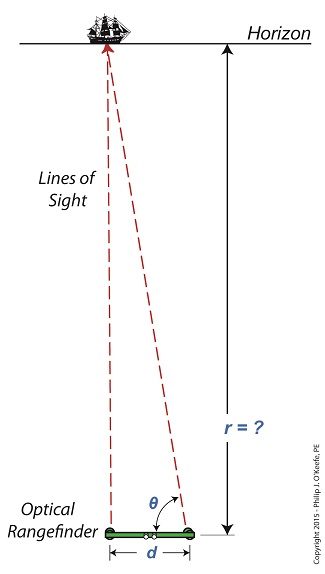
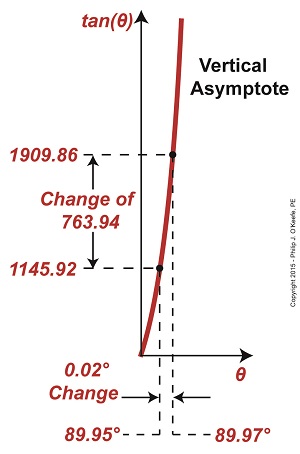
Last time we touched on the limitations of optical rangefinders when attempting to measure extremely long distances. Today we’ll expand on that theme. Let’s say we want to use a rangefinder to determine the distance, r, to an object that’s extremely far away, like a ship on a distant horizon, as shown in Figure 1. Figure 1 It’s obvious that the rangefinder’s length, d, is extremely small in comparison to the total distance viewed, r. When this situation exists, a very long and narrow right triangle is formed between the lines of sight provided by mirrors A and B of the rangefinder, represented by two red dashed lines, and the length of the rangefinder itself, d. It’s still a right triangle, a necessary condition to using our rangefinder formula to determine distance, however, when the triangle is an extremely long, narrow one, the angle θ approaches 90° in value. As discussed in a previous article, a θ value of 90° is impossible for the rangefinder distance formula to work with. The more distant the ship, the longer and narrower the triangle becomes, causing θ to creep ever closer to 90°. From a trigonometric point of view, this spells trouble. The problem is, the closer θ gets to 90°, the greater the disparity potential in its measurement. For example, let’s suppose that when the ship is first sighted with the rangefinder θ is measured at 89.95°. Then a second later the same person seeks to verify his measurement. Without noticing that he’s doing it, he shifts weight on his foot ever so slightly, takes a second reading, and finds that this time θ is 89.97°. That’s a difference of only 0.02° between readings, but it produces a huge change in the tan(θ). Figure 2 represents a graph of these two measurements, with the angle θ values on one axis, the tan(θ) values on the other. Figure 2 The graph illustrates how this minute change in θ of only two hundredths of a degree (0.02°) results in a correspondingly huge change to tan(θ) of 763.94 units. We know that the rangefinder’s length, d, equals 3 feet, so plugging all the numbers into our rangefinder formula we determine the distance to the ship to be, r = d × tan(θ) r = 3 feet × 763.94 = 2291.82 feet What this means on a practical usability level is that when the rangefinder’s adjustable mirror B moves only two one hundredths of a degree, it results in a change to the distance viewed, r, of almost half a mile! There’s another problem that goes hand in hand with the one presented today. We’ll explore it next time.
____________________________________
|
Posts Tagged ‘vertical asymptote’
Limitations of an Optical Rangefinder
Monday, March 23rd, 2015Vertical Asymptotes and Optical Distance Measurement
Friday, March 13th, 2015|
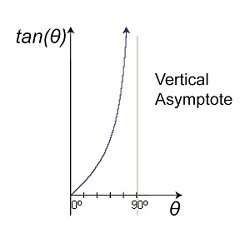
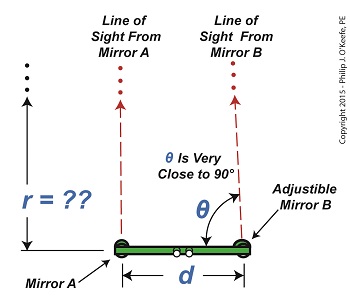
Last time we introduced the vertical asymptote and the fact that it’s associated with the tangent function when angles approach 90° in value. On a graph that looks like this: Figure 1This asymptotic relationship exists when attempting to use an optical rangefinder to determine the distance to objects that are extremely far away– as in so far away they can barely be seen by the naked eye. When this is the case, is it even possible to use the optical rangefinder? Theoretically, yes. But not without complications. Our attempt to use the rangefinder to do this is illustrated in Figure 2. Figure 2You’ll note that the lines of sight extending from mirrors A and B on our rangefinder are almost parallel to each other, creating a situation where a vertical asymptote will form with regard to θ’s tangent. In plain English this means that even minute changes in θ will result in huge changes to tan(θ). We’ll explore that subject next time.
____________________________________
|