|
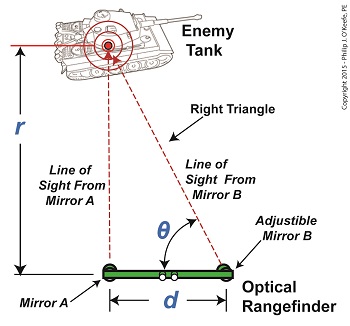
We left off with an artillery soldier spotting an enemy tank in the distance. Luckily, he’s got an optical rangefinder at his disposal to measure the distance between them and crank out an accurate shot. His first action is to peer through the rangefinder’s eyepieces, rotating the adjustable mirror on the right eyepiece until the tank comes into focus. The two lines of sight provided by the left and right eyepieces of the rangefinder form a right triangle due to the parallax effect. One of the angles in this triangle is designated on the illustration by the angle θ, and that’s the angle we’ll be working with. The fact that a right triangle exists means the distance, r, to the tank can be easily measured using principles found in trigonometry, a branch of mathematics that addresses the properties of triangles, hence, the prefix tri in its name. Tangent, and other trigonometric functions like sine and cosine, relate the angles of a right triangle to the ratios of the lengths of the sides of the triangle. In our case we’re concerned with the tangent, which is simply the value that’s derived by dividing the length of the side opposite to the angle θ by the length of its adjacent side. This value can be found in most trigonometry textbook tables, but is most easily found by using a calculator. Simply enter the angle θ‘s value, then press the TAN button. So how does the artillery soldier determine θ‘s value? With the tank in clear focus, it’s easily measured with an indicator gauge attached to the adjustable mirror near the right eyepiece on an optical rangefinder. Our soldier reads the gauge and determines that θ is equal to 89.935°, so the tangent of θ is equal to: tan(θ) = tan(89.935°) = 881.473 Now that we’ve determined the values for d and the tangent of the angle θ, we can plug those numbers into our equation to determine r, the distance to the enemy tank using the equation, r = d × tan(θ) Plugging in numerical values, the equation becomes, r = 3 feet × 881.473 = 2644.419 feet The distance to the tank is 2644.419 feet. Next time we’ll see how the peculiarities of the tangent function place limitations on the accuracy of optical rangefinders over extremely long distances. ____________________________________
|
Engineering Expert Witness Blog
Published by Philip J. O'Keefe, PE, MLE