|
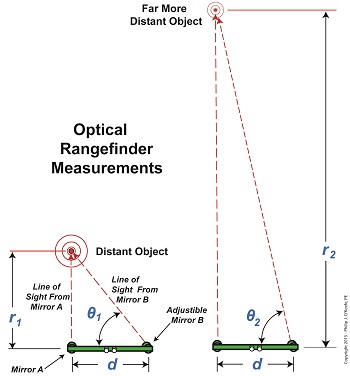
Imagine working, working, working towards a goal and getting oh so close, but never being able to actually reach it. It’s happened to all of us some of the time, but with vertical asymptotes it happens all of the time. We’ll see why the nature of vertical asymptotes presents a problem when measuring extreme distances in today’s blog. We’ve found that optical rangefinders can be useful in measuring long distances. They work well in many situations, but not all. When it comes to extremely long distances they aren’t at all helpful. That’s due to problems presented by trigonometry, more specifically the tangent function and how it leads to vertical asymptotes. Let’s look at Figure 1 to bear this out. Figure 1
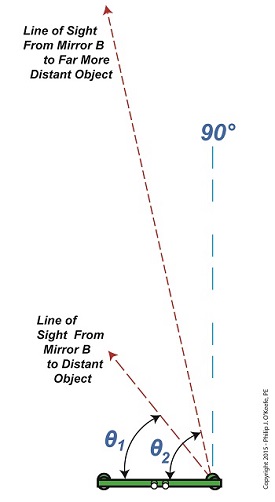
In Figure 1 we see the same rangefinder being used to view objects at two different distances, one distance far greater than the other. There’s an obvious difference in the lengths of the sides of the triangles formed, as well as an obvious difference in angles θ1 and θ2. θ2 is much steeper than θ1. This is more apparent when the lines of sight are isolated, as shown in Figure 2. Figure 2
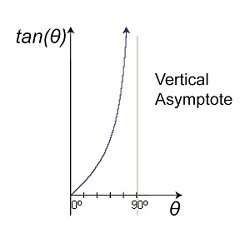
Figure 2 shows that as an object becomes more distant and r, the distance to the object viewed increases, the angle θ gets closer and closer to a value of 90°. What’s significant about this is that a θ value of 90° is impossible for a rangefinder to work with. Why? Because it uses trigonometry to measure distances, more specifically the tangent function within trigonometry, and when θ takes on a value of 90°, it becomes asymptotic in nature — a situation which renders the optical rangefinder useless. To visualize this, we’ve plotted the tangent function for an array of angle θ values on a graph in Figure 3. Figure 3
The curved line represents plotted tangent values for θ that fall between 0° and 90°. What it demonstrates is that as θ gets closer to becoming 90°, it becomes more vertical and steeper in incline. In other words, it forms a vertical asymptote, stretching to reach a value of 90° but never actually getting there. In the math world this means that the tangent’s value is on its way to becoming unbounded or undefined. In plain English this means that the tangent’s value becomes increasingly more unworkable. In fact, the tangent of 90° degrees does not exist. Try entering the number 90 into your calculator and pressing the TAN button. You’ll receive an error message in return. Next week we’ll see the impact this has on the function of an optical rangefinder when the object viewed is so far away the angle θ approaches a value of 90°.
____________________________________
|
Engineering Expert Witness Blog
Published by Philip J. O'Keefe, PE, MLE