|
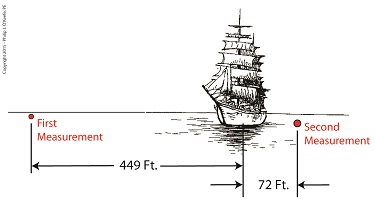
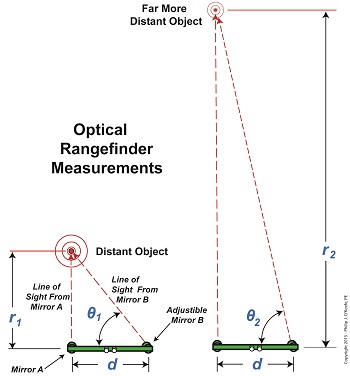
Last time we touched on the fact that bigger is better when it comes to using a rangefinder to measure extremely long distances. Today we’ll expand on that theme and discover how bigger is indeed more accurate. Returning to our previous example, we’re still trying to find the distance to that ship on the horizon. We’ve got two rangefinders at our disposal, one short, one long, and the measurements provided by them are vastly different. Which is correct? To find out, we’ll hypothesize that we’ve taken the time to meticulously measure the distance the hard way, with a really long tape measure. Doing so, we find the actual distance to the ship is 5280 feet. We can now compare the actual measured distance to the measurements taken with our two rangefinders and compare their accuracy: Rangefinder One = 5729 feet – 5280 feet = 449 feet Rangefinder Two = 5208 feet – 5280 feet = -72 feet The smaller rangefinder results in a difference, or error, of 449 feet, while the bigger results in a difference of 72 feet. It’s clear that the bigger rangefinder gets us closer to the actual measurement taken by tape measure, so it’s the most accurate. The obvious conclusion is that the bigger the rangefinder used, the smaller the error factor. That’s because as the length of the rangefinder increases, the smaller the angle θ becomes, a situation which results in the tangent of θ moving farther away from rather than closer to 90°, all of which translates to more accuracy in our rangefinder’s measurements. Put another way, the bigger the rangefinder, the less likelihood there is of its angle θ‘s tangent hovering near 90° and becoming asymptotic, an undesirable outcome for reasons explained in a previous blog in this series. Next time we’ll see how early astronomers were able to arrive at relatively accurate calculations of the distances between Earth and other heavenly bodies by using the parallax effect produced by the world’s largest optical rangefinder, Planet Earth itself. ____________________________________
|
Posts Tagged ‘asymptote’
Optical Rangefinders, Bigger is More Accurate
Tuesday, April 14th, 2015Further Limitations of an Optical Rangefinder
Monday, March 30th, 2015|
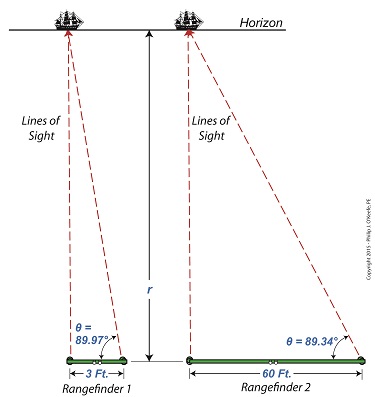
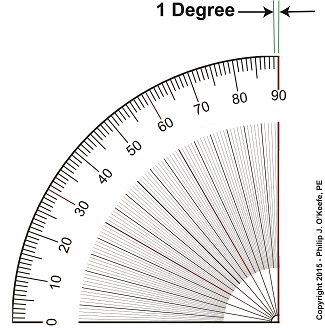
Last time we discovered that when optical rangefinders are used to measure the distance to objects extremely far away we encounter problems. We discussed one of them last time, the fact that as θ approaches 90° the tangent of θ becomes asymptotic, resulting in a situation where even the most minute changes to θ bring about huge corresponding changes to the distance, r, we seek to measure. This difficulty goes hand in hand with another we’ll be discussing today, the problem of very tight spaces. They both lead to a greater potential for measurement inaccuracies. The rangefinder in Figure 1 depicts the kind of situation that often results when attempting to measure objects that are extremely far away, like a ship on a distant horizon. Angle θ is very close to being 90°. Let’s see what that does to our measuring attempts with the rangefinder’s on-board measuring scale, its indicator gauge. The fact is, when a rangefinder’s indicator gauge hovers near 90°, it becomes user unfriendly. To illustrate, let’s refer to a common everyday protractor, shown in Figure 2. Protractors are divided into 1° gradations, which allow us to measure angles between 0° and 90°. This interval is fine for many angle measuring purposes, but we’ll see in a moment why it doesn’t work when measuring extremely long distances. A similar protractor is found on a rangefinder’s indicator gauge, enabling us to measure the angle θ. Notice how small the space is between 89 and 90 degrees. Now imagine having to split that area into hundreds, even thousands, more gradations in order to accurately assess the value of θ. This is precisely the situation we encounter when using a rangefinder to measure extremely long distances where the lines of sight form long, narrow triangles and θ hovers near 90°. Are you beginning to see — or rather not see — the problem? When this situation exists, ultra fine gradations must be made between the 89th and 90th degrees in order to make an accurate measurement of θ . This results in a situation where gradation marks are spaced so closely together they become difficult, if not impossible, for the unaided human eye to read. Next time we’ll see why bigger is indeed better when seeking to solve this problem. ____________________________________
|
Tangent and the Vertical Asymptote
Monday, March 2nd, 2015|
Imagine working, working, working towards a goal and getting oh so close, but never being able to actually reach it. It’s happened to all of us some of the time, but with vertical asymptotes it happens all of the time. We’ll see why the nature of vertical asymptotes presents a problem when measuring extreme distances in today’s blog. We’ve found that optical rangefinders can be useful in measuring long distances. They work well in many situations, but not all. When it comes to extremely long distances they aren’t at all helpful. That’s due to problems presented by trigonometry, more specifically the tangent function and how it leads to vertical asymptotes. Let’s look at Figure 1 to bear this out. Figure 1
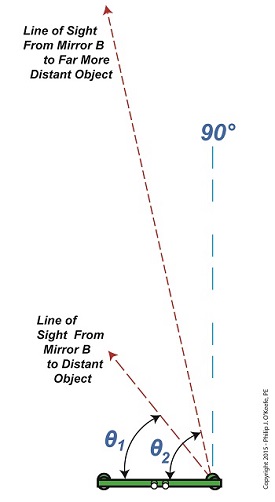
In Figure 1 we see the same rangefinder being used to view objects at two different distances, one distance far greater than the other. There’s an obvious difference in the lengths of the sides of the triangles formed, as well as an obvious difference in angles θ1 and θ2. θ2 is much steeper than θ1. This is more apparent when the lines of sight are isolated, as shown in Figure 2. Figure 2
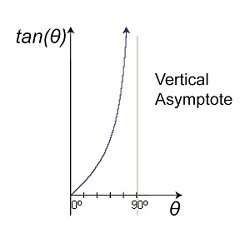
Figure 2 shows that as an object becomes more distant and r, the distance to the object viewed increases, the angle θ gets closer and closer to a value of 90°. What’s significant about this is that a θ value of 90° is impossible for a rangefinder to work with. Why? Because it uses trigonometry to measure distances, more specifically the tangent function within trigonometry, and when θ takes on a value of 90°, it becomes asymptotic in nature — a situation which renders the optical rangefinder useless. To visualize this, we’ve plotted the tangent function for an array of angle θ values on a graph in Figure 3. Figure 3
The curved line represents plotted tangent values for θ that fall between 0° and 90°. What it demonstrates is that as θ gets closer to becoming 90°, it becomes more vertical and steeper in incline. In other words, it forms a vertical asymptote, stretching to reach a value of 90° but never actually getting there. In the math world this means that the tangent’s value is on its way to becoming unbounded or undefined. In plain English this means that the tangent’s value becomes increasingly more unworkable. In fact, the tangent of 90° degrees does not exist. Try entering the number 90 into your calculator and pressing the TAN button. You’ll receive an error message in return. Next week we’ll see the impact this has on the function of an optical rangefinder when the object viewed is so far away the angle θ approaches a value of 90°.
____________________________________
|