|
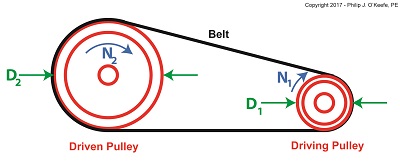
Last time we saw how pulley diameter governs speed in engineering scenarios which make use of a belt and pulley system. Today we’ll see how this phenomenon is defined mathematically through application of the Pulley Speed Ratio Formula, which enables precise pulley diameters to be calculated to achieve specific rotational speeds. Today we’ll apply this Formula to a scenario involving a building’s ventilating system. The Pulley Speed Ratio Formula is, D1 × N1 = D2 × N2 (1) where, D1 is the diameter of the driving pulley and D2 the diameter of the driven pulley. A Pulley Speed Ratio Formula Application
The pulleys’ rotational speeds are represented by N1 and N2, and are measured in revolutions per minute (RPM). Now, let’s apply Equation (1) to an example in which a blower must deliver a specific air flow to a building’s ventilating system. This is accomplished by manipulating the ratios between the driven pulley’s diameter, D2, with respect to the driving pulley’s diameter, D1. If you’ll recall from our discussion last time, when both the driving and driven pulleys have the same diameter, the entire assembly moves at the same speed, and this would be bad for our scenario. An electric motor and blower impeller moving at the same speed is problematic because electric motors are designed to spin at much faster speeds than typical blower impellers in order to produce desired air flow. If their pulleys’ diameters were the same size, it would result in an improperly working ventilating system in which air passes through the furnace heat exchanger and air conditioner cooling coils far too quickly to do an efficient job of heating or cooling. To bear this out, let’s suppose we have an electric motor turning at a fixed speed of 3600 RPM and a belt-driven blower with an impeller that must turn at 1500 RPM to deliver the required air flow according to the blower manufacturer’s data sheet. The motor shaft is fitted with a pulley 3 inches in diameter. What pulley diameter do we need for the blower to turn at the manufacturer’s required 1500 RPM? In this example known variables are D1 = 3 inches, N1 = 3600 RPM, and N2 = 1500 RPM. The diameter D2 is unknown. Inserting the known values into equation (1), we can solve for D2, (3 inches) × (3600 RPM) = D2 × (1500 RPM) (2) Simplified, this becomes, D2 = 7.2 inches (3) Next time we’ll see how friction affects our scenario.
Copyright 2017 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________ |