|
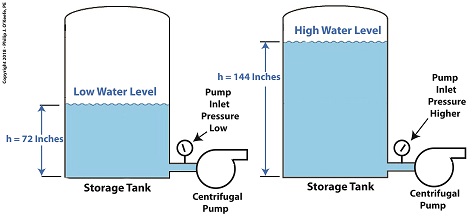
Last time we learned that the risk of damaging cavitation bubbles forming at a centrifugal pump’s inlet can be eliminated by simply increasing the water level inside the tank. Today we’ll do the math that demonstrates how reducing cavitation can be accomplished by raising tank elevation. Reducing Cavitation by Raising Tank Elevation–Before
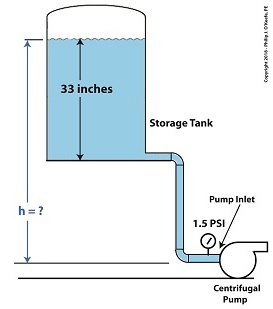
In our example we’ll suppose that we’re having a problem with cavitation bubbles forming at the inlet, where water temperature is 108ºF and water level inside the tank stands at 33 inches. We are using the formula, P = γ × h (1) Equation (1) was introduced previously to correlate water pressure, P, with the specific weight of water, (0.036 pounds/inch3), and the height, h, of the water surface in the tank. If h is 33 inches, then we obtain, P = (0.036 pounds/inch3) × (33 inches) = 1.2 pounds/inch2 (2) So, the weight of the water in the tank exerts a pressure of 1.2 pounds per square inch (PSI) at the bottom of the tank and the pump inlet when it sits at the same elevation as the tank. We know that if we increase the water depth in the tank relative to the pump inlet, we can raise the pressure at the pump inlet in accordance with equation (1). Raising the pressure will eliminate the cavitation bubbles that can form there. But, our tank is of fixed volume, and we can’t add more water to raise water depth beyond 33 inches. However, we can increase the elevation of the tank with respect to the inlet, which will produce the same effect. We’ll use equation (1) to determine the tank elevation, h, that will provide the needed increase. Referring to the thermodynamic properties of water as found in tables appearing in engineering texts, we determine that if we keep water temperature at 108ºF but raise the pressure at the pump inlet from 1.2 PSI to 1.5 PSI, while maintaining current water depth in the tank, cavitation will cease. In other words, we need to increase P by 0.3 PSI. Example of Reducing Cavitation by Tank Elevation–After
Plugging our known values into equation (1) we solve for h, 0.3 PSI = 0.036 pounds/inch3 × h (3) h = 0.3 PSI ÷ 0.036 pounds/inch3 (4) h = 8.3 inches (5) Cavitation will cease when we elevate the tank by 8.3 inches with respect to the pump. Yet another means of increasing inlet pressure is to install a booster pump. We’ll talk about that next time. Copyright 2018 – Philip J. O’Keefe, PE Engineering Expert Witness Blog ____________________________________
|