Posts Tagged ‘thermodynamics’
Monday, May 14th, 2018
|
In our last article, we looked at an example problem involving a cavitating centrifugal pump that was drawing water from a storage tank. The bottom of the storage tank was sitting at the same level as the centrifugal pump’s inlet. The water level in the tank could not be increased to raise the pump inlet pressure, and thus eliminate the cavitation. So, the problem was solved by elevating the tank with respect to the pump inlet. Okay, what if the tank could not be elevated? How do we stop the centrifugal pump from cavitating? Well, we can install a booster pump between the tank and the centrifugal pump.
A booster pump is, as its name implies, a special kind of pump that is used to boost, or raise, water pressure flowing in a pipe. With regard to our example problem in the preceding article, the cavitating centrifugal pump inlet water is at 108ºF and a pressure of 1.2 pounds per square inch (PSI).

Reducing Cavitation With A Booster Pump — Before
Referring to the thermodynamic properties of water as found in tables appearing in engineering texts, we determine that if we keep water temperature at 108ºF but raise the pressure at the pump inlet from 1.2 PSI to 1.5 PSI we can stop the centrifugal pump from cavitating. We can install a booster pump to boost the pressure by the required 0.3 PSI and say goodbye to our cavitation problems.
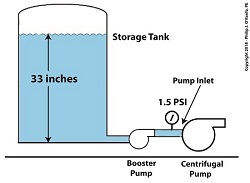
Reducing Cavitation With A Booster Pump — After
This wraps it up for our series on cavitation in pumps. Next time, we’ll begin learning about some different topics.
Copyright 2018 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: booster pump, cavitation, centrifugal pump, engineering, pump inlet pressure, thermodynamics, water pressure, water tank elevation, water tank level, water temperature
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on Reducing Cavitation With A Booster Pump
Monday, May 7th, 2018
|
Last time we learned that the risk of damaging cavitation bubbles forming at a centrifugal pump’s inlet can be eliminated by simply increasing the water level inside the tank. Today we’ll do the math that demonstrates how reducing cavitation can be accomplished by raising tank elevation.

Reducing Cavitation by Raising Tank Elevation–Before
In our example we’ll suppose that we’re having a problem with cavitation bubbles forming at the inlet, where water temperature is 108ºF and water level inside the tank stands at 33 inches. We are using the formula,
P = γ × h (1)
Equation (1) was introduced previously to correlate water pressure, P, with the specific weight of water, (0.036 pounds/inch3), and the height, h, of the water surface in the tank. If h is 33 inches, then we obtain,
P = (0.036 pounds/inch3) × (33 inches) = 1.2 pounds/inch2 (2)
So, the weight of the water in the tank exerts a pressure of 1.2 pounds per square inch (PSI) at the bottom of the tank and the pump inlet when it sits at the same elevation as the tank.
We know that if we increase the water depth in the tank relative to the pump inlet, we can raise the pressure at the pump inlet in accordance with equation (1). Raising the pressure will eliminate the cavitation bubbles that can form there. But, our tank is of fixed volume, and we can’t add more water to raise water depth beyond 33 inches. However, we can increase the elevation of the tank with respect to the inlet, which will produce the same effect. We’ll use equation (1) to determine the tank elevation, h, that will provide the needed increase.
Referring to the thermodynamic properties of water as found in tables appearing in engineering texts, we determine that if we keep water temperature at 108ºF but raise the pressure at the pump inlet from 1.2 PSI to 1.5 PSI, while maintaining current water depth in the tank, cavitation will cease. In other words, we need to increase P by 0.3 PSI.
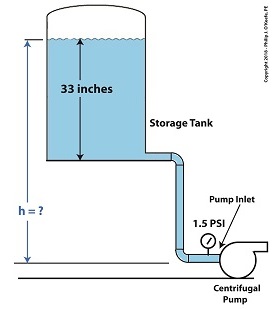
Example of Reducing Cavitation by Tank Elevation–After
Plugging our known values into equation (1) we solve for h,
0.3 PSI = 0.036 pounds/inch3 × h (3)
h = 0.3 PSI ÷ 0.036 pounds/inch3 (4)
h = 8.3 inches (5)
Cavitation will cease when we elevate the tank by 8.3 inches with respect to the pump.
Yet another means of increasing inlet pressure is to install a booster pump. We’ll talk about that next time.
Copyright 2018 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________
|
Tags: cavitation, centrifugal pump, engineering, pump inlet, specific weight of water, stopping cavitation, thermodynamics, water depth, water pressure, water tank elevation
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, power plant training, Product Liability, Professional Malpractice | Comments Off on Reducing Cavitation by Raising Tank Elevation
Monday, April 9th, 2018
|
As we learned previously, cavitation bubbles form at a centrifugal pump’s inlet when the thermodynamic properties of water, namely temperature and pressure, are right. Today we’ll see how just manipulating water temperature can control cavitation.

Manipulating Water Temperature to Control Cavitation
Some centrifugal pumps draw water from an external heat source such as a heat exchanger in order to provide heat to buildings, generate power, and perform manufacturing processes. On some exchangers heat is applied at a fixed rate and can’t be varied. On others heat can be varied by using a heat exchanger fitted with a temperature control. This makes it easy to reduce or lower water temperature introduced at the pump’s inlet. If the temperature is kept low enough relative to the pressure at the inlet, cavitation bubbles won’t form.
Let’s say water enters the pump’s inlet from a heat exchanger at 59ºF and internal pump pressure is 0.25 pounds per square inch (PSI). With these parameters in place water boils and cavitation bubbles will form in the pump inlet. But if the heat exchanger is adjusted so that temperature is lowered by a mere two degrees to 57ºF, cavitation ceases. This is in accordance with the boiling points of water, listed for various pressures and temperatures, as published in engineering thermodynamic texts.
If it’s not possible to lower water temperature at the pump inlet, an alternate method to control cavitation is to raise water pressure, which can be accomplished in different ways. We’ll review those options next time.
Copyright 2018 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: cavitation, centrifugal pump, engineering, heat exchanger, pressure, temperature, temperature control, thermodynamics
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on Manipulating Water Temperature to Control Cavitation
Sunday, January 28th, 2018
|
Last time we learned how the thermodynamic properties of water contribute to the phenomenon of cavitation, and how liquids exist in three states, solid, liquid, or vapor, depending on temperature and surrounding air pressure. Our example of an open pot of water being heated on a stove demonstrated that once water temperature rose above 212ºF, it changed to steam, which initiated the cavitation process. Today we’ll see how decreasing pressure contributes to cavitation.
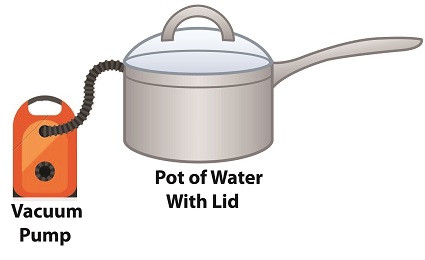
How Decreasing Pressure Contributes to Cavitation
Cavitation can occur without a heat source. In our pot example, we can start the cavitation process by simply decreasing the pressure of the air resting on top of the water, thereby also decreasing the water’s pressure.
Normally atmospheric pressure on Earth exists at around 15 pounds per square inch (PSI). But if we introduce a vacuum pump to an enclosed space, we can create an internal pressure which is lower than the surrounding atmospheric pressure outside the pot. In other words, we create a vacuum. A vacuum is any air pressure lower than atmospheric pressure. This vacuum environment produces an entirely new set of circumstances under which cavitation can occur. In fact, creating a vacuum makes it possible to boil water without using any heat!
As we learned in a past blog on the different forms of heat energy, the boiling point of water varies depending on the location of the stovetop, whether it’s in a place of low altitude, like New Orleans, or higher altitude, like Denver. But if we apply a tight lid to the pot and isolate its internal atmosphere from surrounding atmospheric pressure, you create a closed environment. This allows us to manipulate the pot’s internal pressure. When we attach a vacuum pump to remove air, we reduce the air pressure bearing down on the water inside. With much of the air removed, pressure inside the pot drops below normal atmospheric pressure existing outside the pot, and we discover that at 0.25 PSI water turns to steam at a mere 59ºF and cavitation can begin. That’s right, you can boil water without using heat.
Next time we’ll apply our knowledge of water pressure and temperature to an industrial setting and see how cavitation occurs inside pumps.
opyright 2018 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: atmospheric pressure, cavitation, temperature, thermodynamics, vacuum
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on How Decreasing Pressure Contributes to Cavitation
Monday, January 15th, 2018
|
Last time we introduced the phenomenon of cavitation, which simply stated is the rapid formation and collapse of vapor bubbles within liquids. It’s a destructive force that eats away at the metal parts of water pumps, used in power plants and other industrial settings. To understand how cavitation comes into play, we’ll explore a branch of engineering known as thermodynamics.
Cavitation doesn’t occur in a glass of water resting on a counter, but bring that water to a boil and the cavitation process will begin. That’s because cavitation is initiated when liquids change form from one physical state to another, in this case from a liquid to a vapor we commonly call steam. All liquids exist in three states, namely solid, liquid, and vapor, but in our thermodynamic analysis we’ll only consider two, liquid and vapor, because cavitation can’t occur in solids.

Thermodynamic Properties of Water and Cavitation
At normal atmospheric pressure of 15 pounds per square inch (PSI) which exists in the average kitchen, water remains in a liquid state between the temperatures of 32ºF and 212ºF. Above 212ºF water begins to boil, transforming into steam vapor. The state in which water exists depends on two thermodynamic properties, namely temperature and pressure. Change one of these variables and it affects the other, and thereby the conditions under which cavitation will occur.
We’ll take an in-depth look at this next time when we revisit the topics of pressurization and vacuums.
opyright 2018 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: cavitation, engineering, power plants, pumps, states of water, thermodynamics
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on Thermodynamic Properties of Water and Cavitation
Wednesday, December 4th, 2013
|
Last time we ran our basic power plant steam turbine without a condenser. In that configuration the steam from the turbine exhaust was simply discharged to the surrounding atmosphere. Today we’ll connect it to a condenser to see how it improves the turbine’s efficiency.
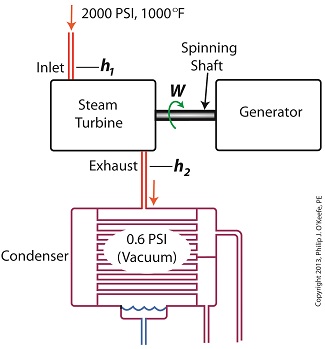
As discussed in a previous blog, enthalpy h1 is solely dependent on the pressure and temperature at the turbine inlet. For purposes of today’s discussion, turbine inlet steam pressure and temperature will remain as last time, with values of 2,000 lbs PSI and 1000°F respectively, and calculations today will be based upon those values. So to review, the inlet enthalpy h1 is,
h1 = 1474 BTU/lb
If the condenser vacuum exists at a pressure of 0.6 PSI, a realistic value for a power plant condenser, then referring to the steam tables in the Van Wylen and Sonntag thermodynamics book, we find that the enthalpy h2 will be,
h2 = 847 BTU/lb
and the amount of useful work that the turbine can perform with the condenser in place would therefore be,
W = h1 – h2 = 1474 BTU/lb – 847 BTU/lb = 627 BTU/lb
So essentially with the condenser present, the work of the turbine is increased by 168 BTU/lb (627 BTU/lb – 459 BTU/lb). To put this increase into terms we can relate to, consider this. Suppose there’s one million pounds of steam flowing through the turbine each hour. Knowing this, the turbine power increase, P, is calculated to be,
P = (168 BTU/lb) ´ (1,000,000 lb/hr) = 168,000,000 BTU/hr
Now according to Marks’ Standard Handbook for Mechanical Engineers, a popular general reference book in mechanical engineering circles, one BTU per hour is equivalent to 0.000393 horsepower, or HP. So converting turbine power, P, to horsepower, HP, we get,
P = (168,000,000 BTU/hr) ´ (0.000393 HP/BTU/hr) = 66,025 HP
A typical automobile has a 120 HP engine, so this equation tells us that the turbine horsepower output was increased a great deal simply by adding a condenser to the turbine exhaust. In fact, it was increased to the tune of the power behind approximately 550 cars!
What all this means is that the stronger the vacuum within the condenser, the greater the difference between h1 and h2 will be. This results in increased turbine efficiency and work output, as evidenced by the greater numeric value for W. Put another way, the turbine’s increased efficiency is a direct result of the condenser’s vacuum forming action and its recapturing of the steam that would otherwise escape from the turbine’s exhaust into the atmosphere.
This wraps up our series on the power plant water-to-steam cycle. Next time we’ll use the power of 3D animation to turn a static 2D image of a centrifugal clutch into a moving portrayal to see how it works.
________________________________________
|
Tags: automobile engine, BTU, BTU/lb, coal power plant, energy, engineering expert witness, enthalpy, forensic engineer, horsepower, mechanical engineer, power, power engineer, power industry expert, power plant efficiency, power plant expert, power plant training instructor, power plant training seminars, steam pressure, steam turbine, steam turbine expert witness, steam water cycle, thermodynamics, vacuum, work
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability, Professional Malpractice | Comments Off on How Condensers Increase Efficiency Inside Power Plants
Tuesday, November 26th, 2013
|
Last time we learned that the amount of useful work, W, that a steam turbine performs is calculated by taking the difference between the enthalpy of the steam entering and then leaving the turbine. And in an earlier blog we learned that a vacuum is created in the condenser when condensate is formed. This vacuum acts to lower the pressure of turbine exhaust, and in so doing also lowers the enthalpy of the exhaust steam. Putting these facts together we are able to generate data which demonstrates how the condenser increases the amount of work produced by the turbine.
To better gauge the effects of a condenser, let’s look at the differences between its being present and not present. Let’s first take a look at how much work is produced by a steam turbine without a condenser.
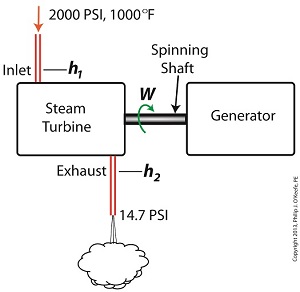
The steam entering the turbine inlet has a pressure of 2000 pounds per square inch (PSI) and a temperature of 1000°F. Knowing these turbine inlet conditions, we can go to the steam tables in any thermodynamics book to find the enthalpy, h1. Titles such as Fundamentals of Classical Thermodynamics by Gordon J. Van Wylen and Richard E. Sonntag list enthalpy values over a wide range of temperatures and pressures. For our example this volume tells us that,
h1 = 1474 BTU/lb
where BTU stands for British Thermal Units, a unit of measurement used to quantify the energy contained within steam or water, in our case the water to steam cycle inside a power plant. Technically speaking, a BTU is the amount of heat energy required to raise the temperature of one pound of water by one degree Fahrenheit. The term lb should be a familiar one, it’s the standard abbreviation used for pound, so enthalpy is the measurement of the amount of energy per pound of steam flowing through, in this case, the turbine.
Since there is no condenser attached to the steam turbine’s exhaust in our illustration, the turbine discharges its spent steam into the surrounding atmosphere. The atmosphere in our scenario exists at 14.7 PSI because our power plant happens to be at sea level. Knowing these facts, the steam tables inform us that the value of the exhausted steam’s enthalpy, h2, is:
h2 = 1015 BTU/lb
Combining the two equations we are able to calculate the useful work the turbine is able to perform as:
W = h1 – h2 = 1474 BTU/lb – 1015 BTU/lb = 459 BTU/lb
This equation tells us that for every pound of steam flowing through it, the turbine converts 459 BTUs of the steam’s heat energy into mechanical energy to run the electrical generator.
Next week we’ll connect a condenser to the steam turbine to see how its efficiency can be improved.
________________________________________
|
Tags: British Thermal Unit, BTU, coal power plant expert, condensate, condenser, engineering expert witness, enthalpy, power engineer, power plant training seminar, pressure, steam, steam power plant, steam tables, steam turbine, steam turbine engineering expert witness, thermodynamics, turbine exhaust steam, vacuum, water, work
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on Enthalpy Values in the Absence of a Condenser
Thursday, November 14th, 2013
|
Last time we learned how the formation of condensate within a power plant’s turbine results in a vacuum being created. This vacuum plays a key role in increasing steam turbine efficiency because it affects a property known as enthalpy, a term used to denote total heat energy contained within a substance. For the purposes of our discussion, that would be the heat energy contained within steam which flows through the turbine in a power plant.
The term enthalpy was first introduced by scientists within the context of the science of thermodynamics sometime in the early 20th Century. As discussed in a previous blog article, thermodynamics is the science that deals with heat and work present within processes. Enthalpy is a key factor in thermodynamics, and is commonly represented in engineering calculations by the letter h and denoted as,
h = u + Pv
where u is the internal energy of a substance, let’s say steam; P is the pressure acting upon a specific volume, v, of the steam; and P and v are multiplied together. Pressure is force per unit area and is measured in psi, pounds per square inch. For the purposes of our discussion, it’s the amount of pressure that steam places on pipes containing it.
Looking at the equation above, simple math tells us that if we increase the pressure, P, the result will be an increase in enthalpy h. If we decrease P, the result will be a decrease in h. Now, let’s see why this property is important with regard to the operation of a steam turbine.
When it comes to steam turbines, thermodynamics tells us that the amount of work they perform is proportional to the difference between the enthalpy of the steam entering the turbine and the enthalpy of the steam at the turbine’s exhaust. What is meant by work is the act of driving the electrical generator, which in turn provides electric power. In other words, the work leads to a useful outcome. This relationship is represented by the following equation,
W = h1 – h2
In terms of the illustration below, W stands for work, or potential for useful outcome of the turbine/generator process in the form of electricity, h1 is the enthalpy of the steam entering the inlet of the turbine from the superheater, and h2 is the enthalpy of the steam leaving at the turbine exhaust.
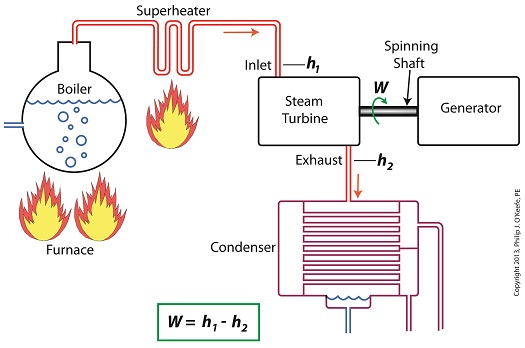
We’ll discuss the importance of enthalpy in more detail next week, when we’ll apply the concept to the work output of a steam turbine.
________________________________________
|
Tags: boiler, coal power plant, condensate, condenser, electrical generator, engineering expert witness, enthalpy difference, forensic engineer, heat energy, internal energy of steam, pipes, power plant design, power plant engineering expert, power plant operation, power plant training, pressure, specific volume of steam, steam pressure, steam turbine, steam turbine work, steam water cycle, superheater, thermodynamics, useful work, vacuum
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on Enthalpy and Steam Turbines
Monday, July 15th, 2013
|
If you took high school chemistry, you learned that water is created when two gases, hydrogen and oxygen are combined. You may have even been lucky enough to have a teacher who was able to perform this magical transformation live during class.
Depending primarily on the amount of heat energy absorbed, water exists in one of the three states of matter, gas, liquid, or solid. Its states also depend on surrounding atmospheric pressure, but more about that later. For our discussion, the water will reside at the atmospheric pressure present at sea level, which is around 14.7 pounds per square inch.
Last time we learned that the heat energy absorbed by water before it begins to boil inside our example tea kettle is known as sensible heat within the field of thermodynamics. The more sensible heat that’s applied, the more the water temperature rises, but only up to a point.
The boiling point of water is 212°F. In fact this is the maximum temperature it will achieve, no matter how much heat energy is applied to it. That’s because once this temperature is reached water begins to change its state of matter so that it becomes steam. At this point the energy absorbed by the water is said to become the latent heat of vaporization, that is, the energy absorbed by the water becomes latent, or masked to the naked eye, because it is working behind the scenes to transform the water into steam.
As the water in a tea kettle is transformed into steam, it expands and escapes through the spout, producing that familiar shrill whistle. But what if we prevented the steam from dispersing into the environment and continued to add heat energy? Ironically enough, under these conditions temperature would continue to rise, upwards of 1500°F, if the stove’s burner were powerful enough. This process is known as superheating. Now hold your hats on, because even more ironically, the heat added to this superheated steam is also said to be sensible heat.
Confused? Let’s take a look at the graph below to clear things up.
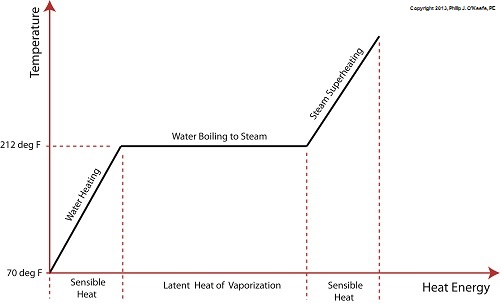
Sensible heat is heat energy that’s added to water, H2O, in its liquid state. It’s also the term used to describe the heat energy added to steam that’s held within a captive environment, such as takes place during superheating. On the other hand, the latent heat of vaporization, that is the heat energy that’s applied to water once it’s reached boiling point, does not lead to a further rise in temperature, as least as measured by a thermometer.
Next time we’ll see how surrounding air pressure affects water’s transition from liquid to steam.
___________________________________________
|
Tags: air pressure, atmospheric pressure, boil, boiler, boiling point, change of state, energy absorbed by water, engineer, engineering expert witness, expands, expert witness, forensic engineer, heat energy, heat transfer, latent heat, power engineering, power plant engineer, sensible heat, steam, steam expansion, superheat, superheating, temperature, temperature rise, thermodynamics, thermometer, water
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training | Comments Off on Forms of Heat Energy – Latent
Sunday, July 7th, 2013
| In our house the whistle of a tea kettle is heard throughout the day, no matter the temp outside. So what produces that familiar high pitched sound?
When a tea kettle filled with room temperature water, say about 70°F, is heating on the stove top, the heat energy from the burner flame will transfer to the water in the kettle and its temperature will steadily rise. This heat energy that is absorbed by the water before it begins to boil is known as sensible heat in thermodynamics. To read more about thermodynamics, click on this hyperlink to one of my previous blog articles on the topic.
So, why is it called sensible heat? It’s so named because it seems to make sense. The term was first used in the early 19th Century by some of the first engineers who were working on the development of boilers and steam engines to power factories and railways. Simply stated, it’s sensible to assume that the more heat you add to the water in the kettle, the more its temperature will rise.
So how high will the temperature rise? Is there a point when it will cease to rise? Good questions. We’ll answer them next week, along with a discussion on another form of heat energy known as the latent heat of vaporization.
___________________________________________
|
Tags: boiler, engineering expert witness, forensic engineer, heat energy, latent heat of vaporization, power plant engineering, sensible heat, steam, temperature, thermodynamics, water
Posted in Engineering and Science, Expert Witness, Forensic Engineering, power plant training | Comments Off on Forms of Heat Energy – Sensible














