|
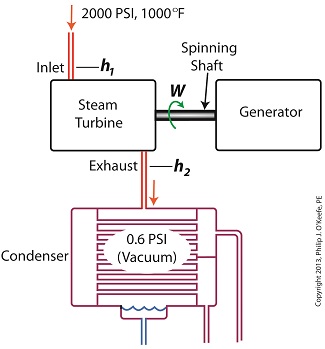
Last time we ran our basic power plant steam turbine without a condenser. In that configuration the steam from the turbine exhaust was simply discharged to the surrounding atmosphere. Today we’ll connect it to a condenser to see how it improves the turbine’s efficiency. As discussed in a previous blog, enthalpy h1 is solely dependent on the pressure and temperature at the turbine inlet. For purposes of today’s discussion, turbine inlet steam pressure and temperature will remain as last time, with values of 2,000 lbs PSI and 1000°F respectively, and calculations today will be based upon those values. So to review, the inlet enthalpy h1 is, h1 = 1474 BTU/lb If the condenser vacuum exists at a pressure of 0.6 PSI, a realistic value for a power plant condenser, then referring to the steam tables in the Van Wylen and Sonntag thermodynamics book, we find that the enthalpy h2 will be, h2 = 847 BTU/lb and the amount of useful work that the turbine can perform with the condenser in place would therefore be, W = h1 – h2 = 1474 BTU/lb – 847 BTU/lb = 627 BTU/lb So essentially with the condenser present, the work of the turbine is increased by 168 BTU/lb (627 BTU/lb – 459 BTU/lb). To put this increase into terms we can relate to, consider this. Suppose there’s one million pounds of steam flowing through the turbine each hour. Knowing this, the turbine power increase, P, is calculated to be, P = (168 BTU/lb) ´ (1,000,000 lb/hr) = 168,000,000 BTU/hr Now according to Marks’ Standard Handbook for Mechanical Engineers, a popular general reference book in mechanical engineering circles, one BTU per hour is equivalent to 0.000393 horsepower, or HP. So converting turbine power, P, to horsepower, HP, we get, P = (168,000,000 BTU/hr) ´ (0.000393 HP/BTU/hr) = 66,025 HP A typical automobile has a 120 HP engine, so this equation tells us that the turbine horsepower output was increased a great deal simply by adding a condenser to the turbine exhaust. In fact, it was increased to the tune of the power behind approximately 550 cars! What all this means is that the stronger the vacuum within the condenser, the greater the difference between h1 and h2 will be. This results in increased turbine efficiency and work output, as evidenced by the greater numeric value for W. Put another way, the turbine’s increased efficiency is a direct result of the condenser’s vacuum forming action and its recapturing of the steam that would otherwise escape from the turbine’s exhaust into the atmosphere. This wraps up our series on the power plant water-to-steam cycle. Next time we’ll use the power of 3D animation to turn a static 2D image of a centrifugal clutch into a moving portrayal to see how it works. ________________________________________ |
Posts Tagged ‘enthalpy’
How Condensers Increase Efficiency Inside Power Plants
Wednesday, December 4th, 2013Enthalpy Values in the Absence of a Condenser
Tuesday, November 26th, 2013|
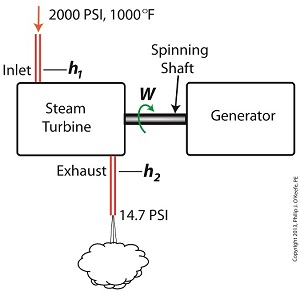
Last time we learned that the amount of useful work, W, that a steam turbine performs is calculated by taking the difference between the enthalpy of the steam entering and then leaving the turbine. And in an earlier blog we learned that a vacuum is created in the condenser when condensate is formed. This vacuum acts to lower the pressure of turbine exhaust, and in so doing also lowers the enthalpy of the exhaust steam. Putting these facts together we are able to generate data which demonstrates how the condenser increases the amount of work produced by the turbine. To better gauge the effects of a condenser, let’s look at the differences between its being present and not present. Let’s first take a look at how much work is produced by a steam turbine without a condenser. The steam entering the turbine inlet has a pressure of 2000 pounds per square inch (PSI) and a temperature of 1000°F. Knowing these turbine inlet conditions, we can go to the steam tables in any thermodynamics book to find the enthalpy, h1. Titles such as Fundamentals of Classical Thermodynamics by Gordon J. Van Wylen and Richard E. Sonntag list enthalpy values over a wide range of temperatures and pressures. For our example this volume tells us that, h1 = 1474 BTU/lb where BTU stands for British Thermal Units, a unit of measurement used to quantify the energy contained within steam or water, in our case the water to steam cycle inside a power plant. Technically speaking, a BTU is the amount of heat energy required to raise the temperature of one pound of water by one degree Fahrenheit. The term lb should be a familiar one, it’s the standard abbreviation used for pound, so enthalpy is the measurement of the amount of energy per pound of steam flowing through, in this case, the turbine. Since there is no condenser attached to the steam turbine’s exhaust in our illustration, the turbine discharges its spent steam into the surrounding atmosphere. The atmosphere in our scenario exists at 14.7 PSI because our power plant happens to be at sea level. Knowing these facts, the steam tables inform us that the value of the exhausted steam’s enthalpy, h2, is: h2 = 1015 BTU/lb Combining the two equations we are able to calculate the useful work the turbine is able to perform as: W = h1 – h2 = 1474 BTU/lb – 1015 BTU/lb = 459 BTU/lb This equation tells us that for every pound of steam flowing through it, the turbine converts 459 BTUs of the steam’s heat energy into mechanical energy to run the electrical generator. Next week we’ll connect a condenser to the steam turbine to see how its efficiency can be improved.
________________________________________ |
Enthalpy and the Potential for More Work
Monday, November 18th, 2013|
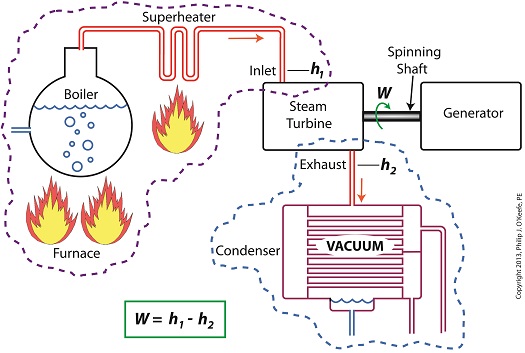
Last time we learned how enthalpy is used to measure heat energy contained in the steam inside a power plant. The higher the steam pressure, the higher the enthalpy, and vice versa, and we touched upon the concept of work, or the potential for a useful outcome of a process. Today we’ll see how to get the maximum work out of a steam turbine by attaching a condenser at the point of its exhaust and making the most of the vacuum that exists within its condenser. Let’s revisit the equation introduced last time, which allows us to determine the amount of useful work output: W = h1 – h2 Applied to a power plant’s water-to-steam cycle, enthalpy h1 is solely dependent on the pressure and temperature of steam entering the turbine from the boiler and superheater, as contained within the purple dashed line in the diagram below. As for enthalpy h2, it’s solely dependent on the pressure and temperature of steam within the condenser portion of the water-to-steam cycle, as shown by the blue dashed circle of the diagram. Next week we’ll see how the condenser, and more specifically the vacuum inside of it, sets the platform for increased energy production, a/k/a work.
________________________________________ |
Superheating, Part 2
Sunday, August 25th, 2013|
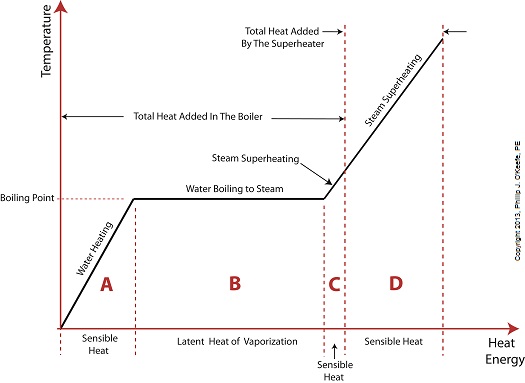
Last time we added a piece of equipment called a superheater, positioned between the boiler and steam turbine, to our basic electric utility power plant steam and water cycle. Its addition enables a greater and more consistent supply of heat energy to the steam which powers the turbine. How much more? Let’s look at Figure 1 to get an idea. Figure 1
You may have noticed that our illustration lacks numerical representation. That’s because power plants are designed differently, depending on fuels used and power output required. So unless we’re talking about a particular power plant, number values would be impractical. For example, I could specify a boiling point of 596°F at 1,500 pounds per square inch (PSI), and a superheater outlet temperature of 1,050°F at 1,200PSI, and I could make note of esoteric things like enthalpy (British Thermal Units per pound mass) values on the Heat Energy axis. But to facilitate our discussion we’ll keep things simple and focus on the general process. Figure 1 shows in phase D the additional heat energy being added to the steam, thanks to the superheater. This is significantly more than had been added by the boiler alone, as represented by phase C. The turbine consumes heat energy added in phases C and D and converts it into mechanical energy to drive the generator, resulting in electrical energy being provided to consumers in the most energy efficient way possible. But increasing power output and efficiency isn’t the superheater’s only job. The heat it adds during phase D ensures the turbine’s safe operation when it’s cranking at full capacity, as represented by the superheated steam zones of phases C and D. Next week we’ll discover how the superheater prevents a destructive process known as condensing from occurring inside the turbine. ________________________________________ |