| Over the last few weeks we looked at the dangers associated with pressurized containers, also known as “pressure vessels.” We also looked at overpressure devices that can keep the pressure from building to the point where the vessel ruptures. But what about keeping pressure vessels from rupturing under normal operating pressure? You know, pressures well below the point where an overpressure device would kick in. This can happen if there is some sort of weakness in the pressure vessel caused by things like poor design, defective materials, or bad welds.
In the 19th Century the machines of the Industrial Revolution were driven by steam. Those magnificent machines advanced our civilization and standard of living. Sounds like a win-win situation, right? Wrong! The downside was that there were no standards for the design of pressure vessels like air storage tanks and boilers. Every engineer had their own ideas as to how they wanted to approach pressure vessel design. I use the word “engineer” loosely because most “engineers” of that time were not college graduates. Some approaches were good, some were bad, and some were in between. The end result was often not good. There were many pressure vessel leaks and explosions that damaged property, caused injury, and took lives. By the turn of the 20th Century industrialization spread far and wide, intensifying safety concerns about pressure vessels. One deadly incident was the straw that broke the camel’s back. On March 10, 1905, the boiler failed in a shoe factory in Brockton, Massachusetts. 58 people were killed and another 117 were injured. The factory was completely destroyed. This tragedy prompted Massachusetts to form a Board of Boiler Rules to write boiler laws. Ohio followed with their own boiler laws. This was a step in the right direction, but each state law was different and a boiler that was legal in one state was illegal in another. There was no standardization between states. In 1911 the American Society of Mechanical Engineers (ASME) formed its Boiler and Pressure Vessel Committee to address the lack of standardization. The committee’s work resulted in publication of the Boiler and Pressure Vessel Code (BPVC). In a nutshell, the BPVC establishes standardized rules governing the design, fabrication, testing, inspection, and repair of boilers and other pressurized vessels and containers. The BPVC set the standards that can be adopted by all states to minimize risk to the public. The ASME is not a government agency, so it cannot enforce compliance with the BPVC. As a matter of fact, compliance with the BPVC by manufacturers has been completely voluntary. However, most state laws now require that pressure vessels must be certified by their manufacturers to be in compliance with the BPVC before they can be sold and put into operation. A certified pressure vessel must be permanently and conspicuously marked with the manufacturer’s name, the date built, serial number, and information about its construction and the type of use it’s designed for. That wraps it up for our series about pressurized containers. Next time, we’ll shift gears and take a look at the project triangle and how it influences the outcome of engineering designs. _____________________________________________ |
Posts Tagged ‘pressure vessel failure’
Pressurized Containers – ASME Boiler and Pressure Vessel Code
Sunday, October 24th, 2010Pressurized Containers
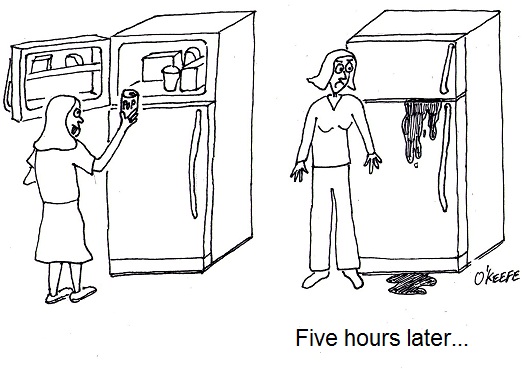
Sunday, September 19th, 2010| My dear daughter is at times forgetful? On one occasion in particular she forgot that she had placed a can of pop in the freezer to speed-chill it. Later that evening when my wife went to get something out of the freezer she was not too pleasantly surprised to find that a black, semi-solid mess had covered most of the freezer’s interior. You got it. The pop can exploded, shooting its pressurized contents all over the place.
You may not have thought much about it before, but pressurized containers are all around us, from pop to aerosol cans, car tires, water heaters, and liquid petroleum gas tanks. Pressurized containers are even more obvious in industrial settings such as oil refineries, power plants, and factories. As its name would imply, pressurized containers, or pressure vessels, are under a lot of pressure, as such, they are no stronger than their weakest point. Whether that point be its sides, as in the case of my daughter’s ruptured pop can, or its ends, weld joints, rivets, or any of the other components that are included in the vessel’s construction. As with anything, the integrity of something is only as good as its weakest part. In an industrial setting, this fact, depending on the vessel’s contents and the severity of the failure, can prove deadly. So what causes pressure in a vessel to get too high? Many factors could be at play, from a safety valve which fails to do its job of relieving excess pressure, to absence of this feature entirely. Many of us learned in grade school science class that when a substance heats up, its molecules vibrate, causing its atoms to want to distance themselves from each other. If this vibrating is taking place within a closed vessel, heated atoms will be prevented from carrying out their desired separation. The result is pressure increases, and along with it the propensity for the weakest points to fail. Whether it’s a slow ooze, high spirited fizz, or outright explosion, the end result is generally the same – it’s a big mess. The behavior of gases in pressurized vessels exposed to heat can be summed up by the Boyle-Charles Law, named after the 17th Century scientist, Robert Boyle, and a 19th Century scientist named Jacques Charles. Both were pioneers in their study of how gases behave under various conditions. The science behind their observations can be summarized into a neat little formula, known as the Boyle-Charles Law for sealed pressure vessels. It looks like this: P1÷T1 = P2÷T2 where P is absolute pressure and T is absolute temperature. What is absolute pressure? It’s the pressure that’s measured when you add the pressure of the air that we live in, our atmosphere, which has been measured to be 14.7 PSI, or pounds per square inch, to whatever pressure you are reading on a pressure gauge. This ultimate pressure is measured at pounds per square inch absolute, or PSIA. Now what is meant by absolute temperature is calculated a little differently. It basically means that you add 460 degrees to the temperature reading on a thermometer. This 460 degrees acts as a kind of fudge factor to keep equations that concern themselves with temperature at or below 0°F to work. The result is said to be in degrees Rankine, and it is denoted by °R. So why do we need this fudge factor? Here’s an example. In the equation above, if temperature is 0°F, then you would be dividing the pressure by zero in the equation above. That’s a no-no in mathematics. Try dividing any number by zero on your calculator and see what I mean. Okay, for those of you who are not mathematically inclined that may not have been very clear. Let’s try a different approach. Probably the best way to show you how the Boyle-Charles Law works is by the following example. Suppose you have a sealed container filled with pressurized gas. The gas is at a temperature of 70°F, and a pressure gauge on the vessel reads 100 PSI. So this condition of pressure and temperature goes into the Boyle-Charles Law equation as P1 = (100 PSI + 14.7 PSI) = 114.7 PSIA and T1 = (70°F + 460) = 530°R. Now let’s introduce a complicating factor. Suppose you leave the container in your car on a hot day. The gas in the container increases in temperature to 150°F. Okay, so this temperature would go into the Boyle-Charles Law equation as T2 = (150°F + 460) = 610°R. Now, suppose the pressure gauge was damaged and the needle fell off. What would the gas pressure in the container be at this temperature? Let’s use the Boyle-Charles Law equation and a little algebra to find out: P1÷T1 = P2÷T2 114.7 PSIA ÷ 530°R = P2÷ 610°R P2 = (114.7 PSIA ÷ 530°R) × 610°R P2 = 132 PSIA = 117.3 PSI What this means is that if the weakest link in a container was made to withstand no more than 110 PSI of pressure, and the pressure inside the vessel in our case has risen to 117.3 PSI, the integrity of our container will be compromised. We’ll return to our vehicle and find a big mess. We’ll continue our discussion of pressure vessels, leaks, and how they can be prevented in the future. _____________________________________________ |