| Ever take a peek inside the toaster while you’re waiting for the toast to pop up? If so, you would have noticed a bright orange glow. That glow is produced when the toasting wires heat up, which in turn creates a nice crusty surface on your bread or waffle. It’s the same phenomenon as when the filament inside an incandescent bulb glows. The light and heat produced in both these cases are the result of the Joule, pronounced “jewel,” effect at work.
To understand Joule heating, let’s first refresh our memories as to electrical current resistance. We learned previously that wire is not a perfect conductor, and as such resistance to flow is encountered. This resistance causes power to be lost along the length of wire, in accordance with this equation: Power Loss = I2 × R Where I is the electric current flowing through a wire, and R is the total electrical resistance of the wire. The power loss is measured in units of Joules per second, otherwise known as watts, “watt” denoting a metric unit of power. It is named after the famed Scottish mechanical engineer, James Watt, who is responsible for inventing the modern steam engine. A Joule is a metric unit of heat energy, named after the English scientist James Prescott Joule. He was a pioneer in the field of thermodynamics, a branch of physics concerned with the relationships between different forms of energy. Anyway, to see how the equation works, let’s look at an example. Suppose we have 12 feet of 12 AWG copper wire. We are using it to feed power to an appliance that draws 10 amperes of electric current. Going to our handy engineering reference book, we find that the 12 AWG wire has an electrical resistance of 0.001588 ohms per foot, “ohm” being a unit of electrical resistance. Plugging in the numbers, our equation for total electrical resistance becomes: R = (0.001588 ohms per foot) × 12 feet = 0.01905 ohms And we can now calculate power loss as follows: Power = I2 × R = (10 amperes)2 × (0.01905 ohms) = 1.905 watts Instead of using a 12 AWG wire, let’s use a smaller diameter wire, say, 26 AWG. Our engineering reference book says that 26 AWG wire has an electrical resistance of 0.0418 ohms per foot. So let’s see how this changes the power loss: R = (0.0418 ohms per foot) × 12 feet = 0.5016 ohms Power = I2 × R = (10 amperes)2 × (0.5016 ohms) = 50.16 watts This explains why appliances like space heaters and window unit air conditioners have short, thick power cords. They draw a lot of current when they operate, and a short power cord, precisely because it is short, poses less electrical resistance than a long cord. A thicker cord also helps reduce resistance to power flow. The result is a large amount of current flowing through a superhighway of wire, the wide berth reducing both the amount of power loss and the probability of dangerous Joule heating effect from taking place. Our example shows that the electric current flowing through the 12 AWG wire loses 1.905 watts of power due to the inconsistencies within the wire, and this in turn causes the wire to heat up. This is Joule heating at work. Joule heating of 50.16 watts in the thinner 26 AWG wire can lead to serious trouble. When using a power cord, heat moves from the copper wire within it, whose job it is to conduct electricity, and beyond, on to the electrical insulation that surrounds it. There the heat is not trapped, but escapes into the environment surrounding the cord. If the wire has low internal resistance and the amount of current flowing through it is within limits which are deemed to be acceptable, then Joule heating can be safely dissipated and the wire remains cool. But if the current goes beyond the safe limit, as specified in the American Wire Gauge (AWG) table for that type of wire, then overheating can be the result. The electrical insulation may start to melt and burn, and the local fire department may then become involved. That’s it for wire sizing and electric current. Next time we’ll slip back into the mechanical world and explore a new topic: the principles of ventilation. _____________________________________________ |
Posts Tagged ‘air conditioner’
Wire Size and Electric Current – Joule Heating
Sunday, March 20th, 2011Thermodynamics in Mechanical Engineering, Part V, Psychrometry
Sunday, January 3rd, 2010|
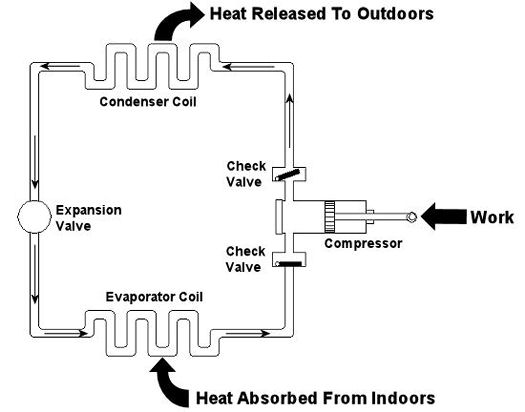
Last week we looked at the arithmetic behind chemical reactions in an area of thermodynamics known as stoichiometry. This week we’ll learn about psychrometry and the value of a summer breeze. Well, more specifically, psychrometry involves the analysis of gas and vapor mixtures, like air and water. You may not have ever heard of psychrometry or psychrometrics, but your body is familiar with it. In fact, it adheres to its principles every time it sweats. See, sweating keeps you cool, and that’s because when liquids like water evaporate, they absorb heat in the process. When sweat, which is mostly water, evaporates from your skin, it takes some of your body heat with it, dissipating it into the atmosphere. That’s why a roomful of sweaty bodies is so uncomfortable to be in. Now let’s say you’re outside and it’s a hot, humid summer day. The air already contains a lot of moisture, so it can’t absorb as much sweat from your body as it would in a drier environment. As a result, your sweat doesn’t evaporate so well. It lingers on your skin, keeping you miserable. Now introduce a summer breeze. The increase of air flow across your skin that it produces serves the same purpose as an electric fan in your home. They both make you cooler by increasing the surrounding air flow, thereby making more air available to contact your skin, and increasing the sweat evaporation process. In the study of psychrometry, mechanical engineers learn about the thermodynamic properties of moist air. Then they use these properties to analyze conditions and design processes which deal with moist air, things like air conditioning systems and dehumidifiers. Let’s return for a moment to that air conditioner example that we used in our discussion of Thermodynamics in Mechanical Engineering, Part III. This is shown in Figure 1 below. Psychrometry would be used here, too. For example, when you are determining how much heat must be removed from the warm, humid air inside your home by the evaporator coil inside your air conditioner. Knowing how much heat must be removed is one of the first steps to designing a system which is properly sized and works efficiently in order to keep you comfortable.
Figure 1 – A Simple Refrigeration Cycle
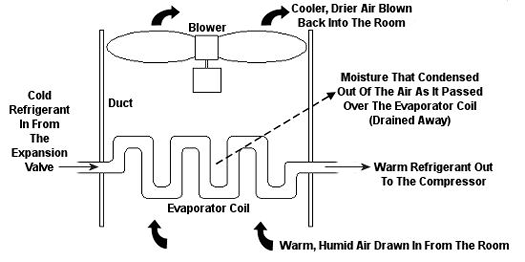
Psychrometric calculations can get pretty involved, and our discussion is meant to provide only a brief overview, but suffice it to say that their basic function is to set up a mass and energy accounting system that adheres to the principles of the First Law of Thermodynamics. In other words, energy and mass going into a system has to add up to energy and mass coming out. Now, let’s return to our discussion on psychrometry in relation to the design of the air conditioning system of Figure 1. Let’s focus on the evaporator coil from this system, as shown in Figure 2. This coil is contained in a duct along with a blower. The air sucked into the evaporator coil from the room has water vapor mixed into it. The pure air part and the water vapor part each contain heat energy. Our bodies perceive that heat energy as warm, humid air. As that humid air is cooled by the evaporator coil, much of the water vapor condenses out of it as liquid moisture, which is then drained out of the air conditioner. What’s left is a cooler mixture of air and greatly reduced water vapor. This mixture then leaves the evaporator coil and is sent back into your home from the duct by way of a blower, resulting in a more comfortable environment for you.
Figure 2 – An Evaporator Coil In An Air Conditioning Unit
So, using the First Law of Thermodynamics, the heat accounting system for the air conditioner looks like this: Qevaporator = (Qair + Qwater vapor)going in – (Qair + Qwater vapor + Qcondensed moisture)going out where, “Qevaporator” is the heat energy removed by the evaporator coil, “Qair” is the heat energy contained in the air, “Qwater vapor” is the heat energy contained in the water vapor, and “Qcondensed moisture” is the heat energy contained in the condensed moisture drained out of the air conditioner. By the way, the letter “Q” is often used to denote heat in thermodynamics. To solve for the equation above, one has to first consider what the pressure, temperature, and relative humidity of the air will be in the room when the air conditioner is first turned on. We must next determine what the desired pressure, temperature and relative humidity should ideally be once the conditioned air leaves the evaporator coil on its journey back into the room. In other words, we need to know the conditions we are starting out with in order to know where we want to end up, comfort-wise. Once these parameters are known, thermodynamic formulas are used to calculate how much heat must be removed by the evaporator coil. Now the air conditioning equipment can be designed with a large enough evaporator coil, with sufficient refrigerant flowing through it, and a large enough blower to efficiently perform the task of keeping us cool. This concludes our tour of the world of thermodynamics. Next week we’ll begin our discussion of an area of mechanical engineering known as fluid mechanics, which is the study of the force, pressure, and energy of both stationary and moving fluids. We’ll see how a hydraulic car jack works, how water flows through pipes, and how airplane wings lift a plane into the sky. _________________________________________________________________ |
Thermodynamics In Mechanical Engineering, Part III, Refrigeration Cycles
Sunday, December 20th, 2009|
Last week we talked about an area of thermodynamics that concerns power cycles, an example of which can be found in a coal fired power plant. This week we’ll learn about another area of thermodynamics, that of refrigeration cycles. It’s been snowing in the Midwest, so the topic seems appropriate enough. A refrigeration cycle is obviously found in your refrigerator, but did you know that it’s also found in your air conditioner? Refrigeration cycles operate in Opposite Land as compared to power cycles. You know, the place where everything works in reverse. Instead of heat going into the cycle and electricity coming out, in a refrigeration cycle, electricity goes in and heat comes out—out of your refrigerator or air conditioned house, that is. Let’s consider an example of the simple air conditioner refrigeration cycle shown in Figure 1. The cycle has four important parts: an evaporator coil, a compressor, a condenser coil, and an expansion valve. All parts are connected by pipes, and the entire system is sealed up tight with refrigerant inside. Figure 1 – A Simple Refrigeration Cycle Used In An Air Conditioner The compressor is the heart of the operation, so to speak. In our simple cycle, the compressor consists of an electric motor-driven piston that moves back and forth within a cylinder. The motor does work as the piston moves back and forth, and the compressor pumps refrigerant through the pipes, the condenser coil, the expansion valve, and the evaporator coil. Like your heart, the pump has check valves that keep refrigerant flowing through the system in one direction (counterclockwise in our example). Keeping the flow going in one direction is critical to the operation of the cycle, as we’ll see in a moment. The refrigerant is the life blood of the cycle. It is a chemical that is manufactured to have special thermodynamic properties. For example, it’s really good at quickly absorbing a lot of heat at low temperature, like the temperature of the air in your house. The evaporator coil in Figure 1 would be located on the inside of your home. As the refrigerant enters the evaporator coil, it is a mixture of liquid and vapor. Inside the evaporator coil, the liquid refrigerant boils off to a vapor as it absorbs heat from the room. Yes, that’s right, the refrigerant boils at room temperature! The heat absorption in the evaporator is helped along by using a fan to push room air across its coil. Warm air from the room gets sucked into the air conditioner and cool air blows out into the room. But that’s not the end of the story. That heat from the room has to somehow get outside of the house, where it can be disposed of. This is so the refrigerant can pick up another load of heat when it flows back through the evaporator coil. But disposing of the heat from the refrigerant isn’t easy, since heat naturally wants to flow from a hotter place to a cooler place. So how do you buck Mother Nature and get heat to flow from the inside of your house where it’s cool to the outside of your house where it’s hotter? It takes work, and that’s where the compressor comes into play. The compressor first pulls the refrigerant vapor out of the evaporator and raises its pressure and temperature. This heart, like our own, is a hard worker. As the vapor leaves the compressor and passes through the condenser coil located outside your home, it is in a state where it can easily give up its heat to the warm air outside. The release of heat is helped along by the use of another fan that serves to push the outdoor air across the outside surfaces of the condenser coil. Then, as heat is released to the outdoor air, the refrigerant condenses back into a liquid. After leaving the condenser coil, the liquid refrigerant passes through the expansion valve, where its pressure and temperature are reduced. The refrigerant is now ready to pick up a new load of heat in the evaporator coil, and the cycle repeats itself with the help of a working electric motor. Next week, we’ll continue our exploration of thermodynamics and narrow our focus onto an area known as stoichiometry, which is concerned with the math behind chemical reactions, like those that take place during the burning of fuels. Math is fun. Just keep repeating that to yourself. _________________________________________________________________ |