|
In this blog series we’ve been examining gear train usefulness, specifically in terms of increasing torque. Equations presented last week began us on the final leg of our journey, and we’ve arrived at the point where the closing combination of equations will demonstrate the loss of speed that takes place when torque is increased within a gear train. To that end, the two main equations under consideration as presented last week, are:
where R is the gear ratio of the gear train, N is the number of gear teeth, n is the gear rotational speed in revolutions per minute (RPM), T is the torque, and D is the gear pitch radius. We were able to link these two equations by working through five key design equations applicable to simplified gear trains. For the full step-by-step progression see last week’s blog. After working through the equations presented last time we were able to arrive at an equation which links equations (1) and (2). Here it is:
If you follow the color coding, you’ll see the elements of equations (1) and (2) which come together in equation (7). Because equation (7) links the gear speed ratios (red) with the gear pitch radii ratios (green), we can set the ratios in equation (1) equal to those in equation (2). Doing so, we get: R = NDriven ÷ NDriving = nDriving ÷ nDriven = DDriven ÷ DDrivng = TDriven ÷ TDriving
In order to see the tradeoff between speed and torque, we need only consider the parts of the equation which concern themselves with factors relating to speed and torque. Removing the other unnecessary factors, we arrive at:
Next week we’ll plug numbers into equation (8) and disclose the tradeoff of speed for torque.
_______________________________________
|
Posts Tagged ‘pitch radius’
Determining the Gear Train Tradeoff of Torque vs. Speed, Part Two
Wednesday, August 20th, 2014Equating Torques and Pitch Circle Radii Within a Gear Train
Thursday, May 29th, 2014|
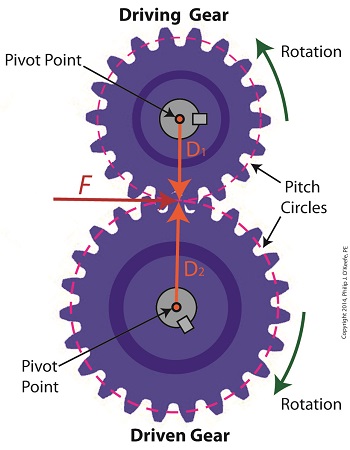
Last time we developed torque equations for the driving and driven gears within a simple gear train. They are, T1 = D1 × F T2 = D2 × F where, T1 and T2 are the driving and driven gear torques, D1 and D2 are the driving and driven gear pitch radii, and F is the resultant Force vector, the common factor between the two equations. Now we’ll combine these two equations relative to F to arrive at a single equation which equates the torques and pitch circle radii of the driving and driven gears in the gear train. This type of computation is commonly used to design gear trains to ensure they perform at a given level. As a first step we’ll use algebra to rearrange terms and place the two equations equal to F. First we’ll do it for the driving gear, dividing both sides of the equation by the pitch circle radius, D1. T1 ÷ D1 = D1 ÷ D1 × F T1 ÷ D1= 1 × F F = T1 ÷ D1 In a similar fashion, we’ll do it for the driven gear by dividing both sides of the equation by the pitch circle radius, D2. T2 = D2 × F → F = T2 ÷ D2 Since F is the common term between the two equations, we can set them up as equal to each other, F = T1 ÷ D1 = T2 ÷ D2 which means that, T1 ÷ D1 = T2 ÷ D2 Next time we’ll see how to use this equation to manipulate our gear train so that it acts as a torque converter by increasing T2 with respect to T1 and the ratio of D1 to D2, thus providing a mechanical advantage to the electric motor the gear train is attached to. _______________________________________ |