|
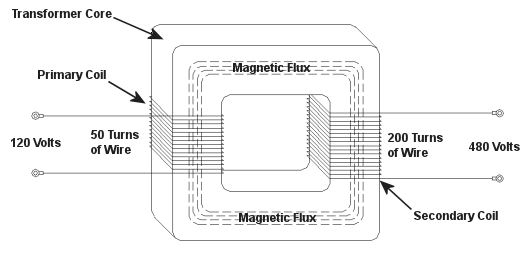
As a child I considered the reindeer Rudolph, with his nose so bright, to be a marvel of engineering. Now an adult, I remain perplexed as to the mystery behind the self-generating power source behind his nose. Did it ever overheat? I wondered. Perhaps today’s discussion can shed some light on the matter. During the course of our discussion of electricity certain terms have been tossed about, like voltage and current. For some the distinction between the two may be unclear, and that is what we’ll be addressing today. Electricity is a rather abstract phenomenon, but you may consider the flow of electrical current through a wire to be much like water flowing through a garden hose. The water won’t flow unless there’s sufficient pressure behind it, and that pressure is supplied by pumps, either at your city water works or your personal well. Take away the pressure, and the water stops flowing through the hose. Electricity flows in much the same manner. It requires a pushing pressure to get it on its journey from power plant to home, and that pressure is voltage. Take away voltage, and the current stops flowing through the wire. Voltage is, of course, produced by an electrical generator at the power plant. Last time we saw how an electrical transformer can reduce high voltage to low voltage and how this process also works in reverse. But how can that be? How can low voltage be turned into high? Is it really possible to get “something from nothing”? Let’s take a closer look. When a light bulb burns out in your home, you routinely look at the bulb to see how many watts it is so you can replace it with the same type. But what exactly is a “watt”? It’s a unit of power, and the markings on the bulb tell you how much electrical power it consumes when you use it. Generally speaking, this electrical power is related to voltage and current by this formula: Power = Volts × Electrical Current Knowing this, if I have a 60 watt bulb in a table lamp, and I plug it into a 120 volt wall outlet, then how much electrical current is the lamp going to draw from the outlet? Using the formula above and a little algebra, we get: Electrical Current = Power ÷ Volts Electrical Current = 60 watts ÷ 120 volts = 0.5 amperes And believe it or not, this same formula that’s used to assess power of a light bulb also applies to electrical transformers. Basically, the power going into the transformer is equal to the power coming out. To see how this works, consider the example step-up transformer shown in Figure 1, which converts a low voltage to a higher one. By the way, “step up” transformers have all sorts of applications. For example, they are used by electric utilities to raise the voltage produced by a power plant to make it more economical to transmit to far away customers. We’ll get into that in another article. Figure 1 – A Step-Up Transformer In this example the input voltage on the primary coil is stepped up from 120 volts to 480 volts on the secondary coil, and this works according to the formula we learned about in last week’s blog: NP ÷ NS = VP ÷ VS where NP and NS are the number of turns of wire in the primary and secondary coils respectively, and VP and VS are the voltages of the primary and secondary coils respectively. Plugging in the numbers we get: 50 turns ÷ 200 turns = 120 volts ÷ VS [(200 turns ÷ 50 turns) × 120 volts] = VS = 480 volts Okay, for the sake of our example let’s say that an electric motor is connected to the 480 volt secondary coil. We have an electric meter hooked up to the primary coil and we measure a 2 ampere (a.k.a. “amps”) electrical current flowing through it. Without having the benefit of another electric meter positioned at the secondary coil, how can we measure how much electrical current is flowing through it? The current flowing through the secondary coil is found by equalizing the power in the primary and secondary coils: PowerP = PowerS Another way of stating this is to say that electrical power is equal to volts times current, so the equation becomes: VP × IP = VS × IS where IP and IS are the primary coil and secondary coil currents, respectively. Plugging in the numbers and working a little algebra we get the electrical current in the secondary coil: 120 volts × 2 amps = 480 volts × IS IS = (120 volts × 2 amps) ÷ 480 volts = 0.5 amps This shows us that the current flowing in the secondary coil is lower than that of the primary coil. It is therefore obvious that the voltage increase in the secondary coil comes at the expense of electrical current that can flow through the secondary coil. Squeeze down on current, voltage goes up. Squeeze down on voltage, current goes up. The power flowing through the transformer stays the same. Conversely, step-down transformers reduce the voltage coming in, and thereby produce the reverse effect. There is an actual increase in current that can flow through the secondary coil. This principle exemplifies the tradeoff process which is often present in science and engineering. Next time we’ll explore how both step-up and step-down transformers are used by electric utilities to transmit power from power plants to its customers tied into the utility grid. As for Rudolph and his power source, that’s still under investigation. _____________________________________________
|
Posts Tagged ‘primary coil’
Transformers – The Voltage/Current Trade-Off
Sunday, December 26th, 2010Transformers – Something To Do With The Flux
Sunday, December 19th, 2010| Aside from the magical manifestation of innumerable top hats and replicate bodies that the movie The Prestige boasts is possible, there are many other fascinating applications of electricity, as we’ll see today.
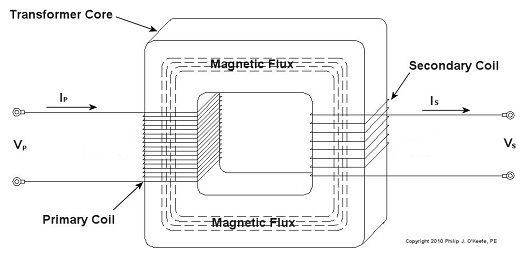
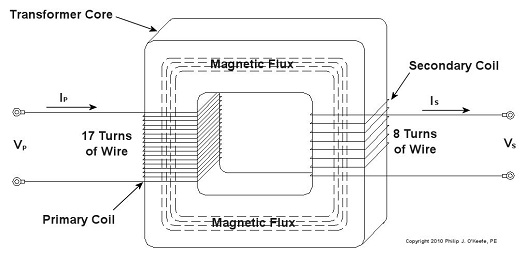
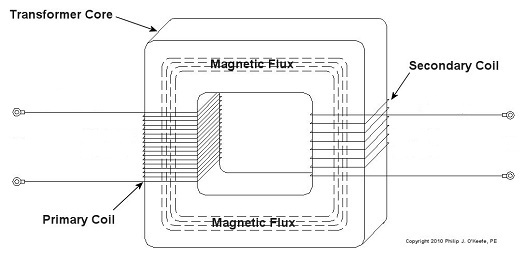
Last time we learned how George Westinghouse’s chief engineer, William Stanley, developed the first practical transformer for electric utility use. Now let’s see how it works, as illustrated in Figure 1. Figure 1 – The Basic Electrical Transformer What we have here is an alternating current (AC) power source. And much like an electrical generator in a utility power plant, it is connected via power lines to the primary coil wires of a transformer, such as the one which feeds power to your house. The voltage applied by the source, that is, the power plant, to the primary coil is known as VP, and the electrical current flowing through the primary coil is referred to as IP. As we learned last week, the continually varying electrical current flowing through the coil creates lines of magnetic flux, which also continually vary. In our diagram the lines of flux flow around the core of the transformer. The magnetic flux present in the core then induces AC voltage, or VS, and current, or IS, to the secondary coil when its wires are connected to something requiring an electrical load to operate. Some examples would be light bulbs, TV’s, and most appliances found in the average home. As was mentioned last week, the number of wire turns, or loops, in the secondary coil as compared to the primary coil determine how the transformer will change the voltage that is applied to it. An example of this phenomenon can be observed in the power lines supplying electricity to our homes. Voltage from power plants is too high to be introduced into our homes, so transformers convert it to a lower voltage, one which can be used by the myriad of electrical devices we couldn’t live without. To get an idea of how this voltage changing works, let’s consider Figure 2. Figure 2 – Basic Transformer Example We can see that the primary coil has 17 turns of wire and the secondary coil has 8. For purposes of our example and to keep the numbers workable, let’s arbitrarily say that VP = 5 volts AC. By the way, the power initially coming into the transformer feeding your home is typically measured in the thousands of volts. Now it’s time to do some math. Based on this input voltage and the number of wire turns in each coil, what would the voltage be on the secondary coil? As William Stanley discovered, it’s a matter of ratios and algebra, and it works according to this formula: NP ÷ NS = VP ÷ VS Here NP and NS are the number of turns of wire in the primary and secondary coils, respectively. So plugging in the numbers we get: 17 turns ÷ 8 turns = 5 volts ÷ VS [(8 turns ÷ 17 turns) x 5 volts] = VS = 2.3 volts This tells us that the transformer in our example reduces, or “steps down” 5 volts AC to just under half the voltage. So the transformer changed a higher voltage to a lower voltage. By the same token, a large utility transformer can be used to reduce transmission line voltage to one which can be used safely within our homes. Like magic, this mechanism also works in reverse. For example, you can apply 2.3volts AC to the 8 turn coil and you will get 5 volts AC out of the 17 turn coil, resulting in a “stepping up” of voltage. But wait a minute. How can you possibly get more voltage out than you put in? Next time we’ll find out. _____________________________________________ |
Transformers – Alternating Current Does the Trick
Sunday, December 12th, 2010| If you’ve seen the movie The Prestige, you know just how “tricky” electricity can be, and if you haven’t seen it yet, you’ve yet to see a great movie. In it, Hugh Jackman uses the magical properties of electricity to pull off a magic trick the likes of which the world has never seen. But that’s all I’ll say about that… see the movie.
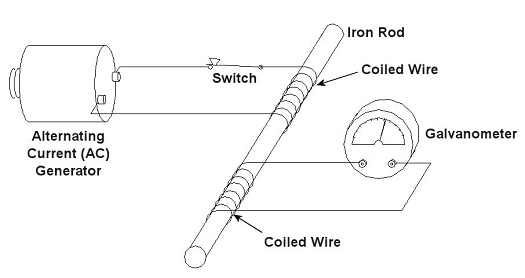
In 1886, a young American inventor named William Stanley did some serious thinking about Michael Faraday, the British scientist we introduced last week, and his work with electricity and magnetism. Stanley figured out how to put it all together. The result was the world’s first electrical transformer. What fueled Stanley’s curiosity? Like most good inventors, he perceived a need and sought to fill it. At the time George Westinghouse was developing his alternating current (AC) electric utility power system, the same basic system we use today. As Westinghouse’s chief engineer, Stanley was given the task of figuring out a way to efficiently change voltage levels on an AC power grid. The industrial revolution was in full swing, and for various industrial purposes factories needed to operate on voltage levels different from those produced by the Westinghouse generators. Stanley approached the task before him with the benefit of knowledge supplied by Faraday’s experimentation. He knew that Faraday was able to cause current to flow through a wire by moving a magnet near it back and forth. This phenomenon occurred because lines of magnetic flux were varying over time with respect to the wire through the magnet’s movement. Being aware of the vicissitudes of alternating current, the way it varies in intensity and direction, Stanley was able to conclude that any lines of magnetic flux generated by AC current flowing through a coiled wire would also tend to vary over time. Armed with this knowledge, Stanley replaced the DC battery used in Faraday’s experiment with an AC generator. This modified setup is shown in Figure 1. Figure 1 – Faraday’s Experiment Modified With An AC Power Source In the modified setup the switch is closed, causing the AC power flowing through the first coiled wire to create lines of magnetic flux in the iron rod. These lines of flux continually vary and thus induce AC flow in the second coil. The action taking place is duly recorded by a Galvanometer needle, which keeps moving so long as the switch remains closed. Stanley also knew that the voltage created in the second coiled wire was dependent on how many turns, or loops, of wire were present in it compared to the number of turns of wire in the first coil. He made the observation that if less turns were present in the second coiled wire as compared to the first, less voltage would also be emitted from the second coiled wire. This demonstrates the phenomenon of changing voltage with respect to supply delivered by the AC generator to the first coil. Putting these findings together, Stanley was able to develop the first practical electrical transformer, whose basic design is shown in Figure 2. Here we see that the iron rod from Faraday’s experiment has been replaced with an iron transformer core resembling a squared off doughnut. Figure 2 – A Basic Electrical Transformer Next time we’ll get into the math behind this discussion, and we’ll see how Stanley’s transformer worked. _____________________________________________ |