|
Last time we discovered that Earth zips around the sun at the mind boggling speed of 29,680 meters per second. This is the final bit of information required to calculate Fg, the gravitational force exerted upon Earth by its sun, as set out in Newton’s equation on the subject and derived from his Second Law of Motion. We’ll calculate that quantity today. Newton’s formula that we’ll be working with is, Fg = [m × v2] ÷ r where Earth’s speed, or orbital velocity, is the v in the equation. The other variables, m and r, have previously been determined in this blog series. For a refresher see Centripital Force Makes the Earth Go Round, What is Earth’s Mass, and Calculating the Distance to the Sun. Earth’s mass, m, is valued at 5.96 × 1024 kilograms, while r is Johannes Kepler’s astronomical unit, equal to about 149,000,000,000 meters. Inserting these numerical values into Newton’s equation to determine the sun’s gravitational force acting upon Earth we arrive at, Fg = [(5.96 × 1024 kilograms) × (29,680 meters per second)2] ÷ 149,000,000,000 meters Fg = 3.52 × 1022 kilogram • meter per second2 This metric unit of force, kilogram • meter per second2, represents kilograms multiplied by meters, and their product divided by seconds squared. It’s known in scientific circles as the Newton, in honor of Sir Isaac Newton, widely recognized as one of the greatest scientists of all time and a key figure in the scientific revolution that began over three centuries ago. Therefore the sun’s gravitational force acting upon Earth is typically referred to as, Fg = 3.52 × 1022 Newtons Here in the US where we like to use English units such as feet and pounds, the Newton is said to equal 0.225 pounds of force. Therefore in English units the sun’s gravitational force is expressed as, Fg = (3.52 × 1022 Newtons) × (0.225 pounds of force per Newton) Fg = 7.93 × 1021 pounds That’s scientific notation for 7,930,000,000,000,000,000,000 pounds! That’s the amount of force exerted by the sun’s gravitational pull on Earth. Seems about right — right? Now that we know Fg, we have everything we need to calculate the mass of the sun, which in turn enables us to determine the mass and gravity of other planets in our solar system. We’ll calculate the sun’s mass next time. ____________________________________
|
Posts Tagged ‘engineering expert witness’
The Sun’s Gravitational Force
Monday, August 3rd, 2015Earth’s High Speed Race Around the Sun
Tuesday, July 28th, 2015|
Last time we began our discussion on velocity by focusing on one of its aspects, distance, and we calculated Earth’s orbital distance around the sun to be 5,816,023,200 miles. Today we’ll focus on velocity’s other aspect, time. Together, these aspects will allow us to solve for Earth’s orbital velocity, aka speed. When early astronomers monitored Earth’s journeys, they found it took exactly one year for it to complete its orbit around the sun. They combined this fact with Earth’s orbital travel distance of 5,816,023,200, or 9.36 × 1011 meters — meters being the unit of measurement most often used in scientific computations — and solved for Earth’s orbital velocity as follows, v = 9.36 × 1011 meters ÷ 1 year = 9.36 × 1011 meters per year The scientific notation of 9.36 × 1011 equates to 936,000,000,000 meters, a large and unruly number to work with. We can simplify things further by breaking this number down into units of meters per second, which will then allow us to arrive at Earth’s velocity in terms of miles per hour, something most Earthlings can relate to. One meter per second is equal to 2.237 miles per hour, and there are 31,536,000 seconds in one year, so breaking Earth’s orbital velocity down into meters per second we arrive at, v = 9.36 × 1011 meters ÷ 31,536,000 seconds = 29,680 meters per second v = (29,680 meters per second) × (2.237 mph/m/sec) = 66,394 miles per hour Yes, it’s true, Earth whips around the sun at warp speed. Our fastest man made rockets only achieve speeds of about 25,000 miles per hour. Earth beats them two-to-one! Now that we know Earth’s orbital velocity, we have everything we need to calculate the gravitational force exerted on Earth by the sun. We’ll do that next time.
____________________________________
|
Earth’s Orbital Velocity
Sunday, July 19th, 2015|
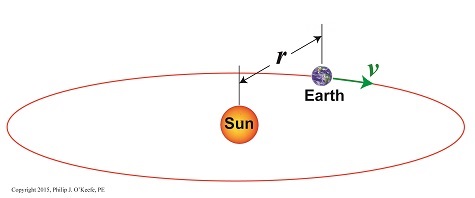
Last time we introduced Newton’s equation to calculate the sun’s gravitational force acting upon Earth, and today we’ll begin solving for the last remaining unsolved variable within that equation, v, Earth’s orbital velocity. Here again is Newton’s equation, Fg = [m × v2] ÷ r For a refresher on how we solved for m, Earth’s mass, and r, the distance between Earth and the sun, follow these links to past blogs in this series, What is Earth’s Mass and Calculating the Distance to the Sun. Velocity, or speed, as it’s most commonly referred to, is based on both time and distance. To bear this out we’ll use an object and situation familiar to all of us, traveling in a car. The car’s velocity is a factor of both the distance traveled and the time it takes to get there. A car traveling at a velocity of 30 miles per hour will cover a distance of 30 miles in one hour’s time. This relationship is borne out by the formula, vCar = distance traveled ÷ travel time vCar = 30 miles ÷ 1 hour = 30 miles per hour Similarly, v is the distance Earth travels during its orbital journey around the sun within a specified period of time. It had been observed since ancient times that it takes Earth one year to complete one orbit, so all that remained to be done was calculate the distance Earth traveled during that time. Vital to calculations was the fact that Earth’s orbit is a circle, which allows geometry to be employed and calculations to be thereby simplified. Refer to Figure l. Figure 1 From geometry we know that the circumference of a circle, C, is calculated by, C = 2× π × r where π is a constant, the well known mathematical term pi, which is equal to 3.1416, and r is the radius of Earth’s circular orbit, determined, courtesy of the work of Johannes Kepler and Edmund Halley, to be approximately 93,000,000 miles. Stated in metric units, the unit of measurement most often employed in science, that comes to 149,000,000,000 meters. Inserting these numerical values for π and r into the circumference formula, scientists calculated the distance Earth travels in one orbit around the sun to be, C = 2 × π × 149,000,000,000 meters = 9.36 x 1011 meters Next time we’ll introduce the time element into our equations and solve for v, and from there we’ll go on and finally solve for Fg, the sun’s gravitational force acting upon Earth.
____________________________________
|
Centripetal Force Makes the Earth Go Round
Thursday, July 9th, 2015|
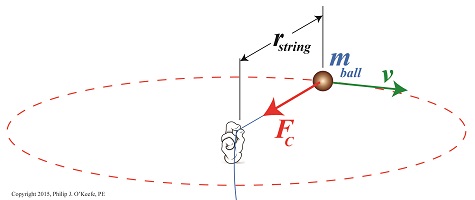
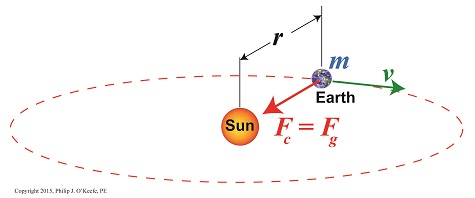
Last time we saw how centripetal force is responsible for keeping a child’s ball moving in a circular path when twirled above his head. Today we’ll see how that same force is responsible for keeping Earth in its rotation around the sun. We’ll use Isaac Newton’s Second Law of Motion as it relates to centripetal force to bear that out today. Our example from last week, Figure 1 According to Newton’s Second Law of Motion, Fc, the centripetal force acting upon the ball, is calculated by the equation, Fc = [mball × v2] ÷ rstring where, mball is the ball’s mass, v the ball’s velocity, and rstring is the length of the string. The mechanics are obviously different with regard to Earth and its orbit around the sun, where there’s no obvious physical link between the objects in rotation. In this case the sun’s gravitational force, Fg, acts to tether Earth to it. And just like the string and ball, the sun’s gravitational tether creates a centripetal force, Fc, which prevents Earth from leaving its orbital path. See Figure 2. Figure 2 Newton concluded that for the Earth to remain on its permanent, fixed path of orbit around the sun, Fc must be equal to Fg, and that the forces in play between the sun and Earth were like a gigantic tug of war where neither side is able to pull any harder than the other. This stalemate is responsible for keeping Earth stably in place in its orbit. According to Newton’s Second Law, the sun’s gravitational force acting upon the Earth is calculated by, Fg = Fc = [m × v2] ÷ r where, m is Earth’s mass, v its orbital velocity, and r the distance between Earth and the sun. Thanks to early scientists like Edmund Halley and Henry Cavendish, the values for m and r had already been determined. That left v, Earth’s orbital velocity, the only variable remaining to be solved. We’ll see how 19th Century scientists accomplished that next time.
____________________________________
|
Calculating the Distance to the Sun
Thursday, June 25th, 2015|
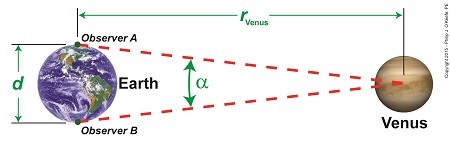
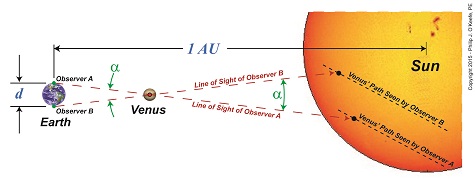
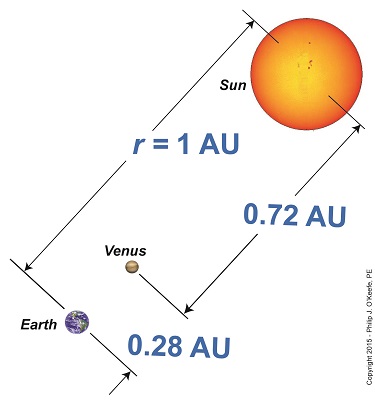
We’ve been paying a lot of attention to Venus and its orbital patterns, as did scientist Edmund Halley hundreds of years ago. Back then he came up with a plan to determine Earth’s distance to the sun, the AU. Two key components were Kepler’s Astronomical Unit, or AU, and an angle, α, which formed between lines of sight followed by observers on Earth during the Transit of Venus. Halley theorized that α together with Kepler’s Third Law of Planetary Motion would make it possible to calculate the AU. We’ll see how today. Figure 1 Figure 1 depicts what Halley had in mind. He theorized that if observers positioned on opposite sides of Earth could determine the precise times it took Venus to travel across the sun’s face from each of their perspectives, they could use this information together with previously gathered information on the time it takes Earth and Venus to make a complete orbit around the sun. This would allow the angle α to be calculated, and from that Earth’s distance to Venus, rVenus. Halley’s calculations for α are beyond the scope of this series, but if you’re interested in reading more about them, you can follow this link. Earth’s distance to Venus, rVenus, is computed in a manner similar to the method we used previously to determine Earth’s distance to the moon, by using this equation, r = d × tan(θ) For a refresher on the subject, follow this link to my past blog on Optically Measuring Cosmic Distances. And here’s the same equation modified to solve for the distance between Earth and Venus, rVenus, rVenus = d ÷ tan(α) (1) Once Earth’s distance to Venus was determined, its value was incorporated into Kepler’s equation for 1 AU, and the distance between Earth and the sun became known. Here again is the equation from Kepler’s Third Law of Planetary Motion, 1 AU = rVenus ÷ 0.28 (2) And here it is with the function for rVenus from equation (1) inserted into equation (2) to solve for 1 AU, 1 AU = [d ÷ tan(α)] ÷ 0.28 1 AU = d ÷ [0.28 × tan(α)] (3) From equation (3) the distance between Earth and the sun, 1 Astronomical Unit, was calculated to be between 92,000,000 and 96,000,000 miles. Unfortunately, a Transit of Venus did not occur within Halley’s lifetime, but scientists that followed him applied his methodology after the next Transit occurred in 1761. Since that time modern technology and the radar have improved measuring accuracy so that we now know the sun is located 92,935,700 miles from Earth. Next time we’ll return full circle to our opening topic in this long blog series when we reopen our discussion on gravity, specifically, how the concept of centripetal force is instrumental in determining the gravitational force exerted upon Earth by the sun.
____________________________________
|
Earth’s Distance to the Sun — A Roadmap
Thursday, June 18th, 2015|
We left off with Edmund Halley’s proposed method to solve the riddle of Earth’s distance to the sun. Halley posited that when Venus’ orbit brought it directly between the Earth and sun, then principles of astronomy, trigonometry, and geometry could be combined to calculate that distance. Instrumental to Halley’s theory were a number of elements discussed previously in this blog series, including the work of Johannes Kepler. We’ll mesh those elements today and chart the course for future discoveries. To begin things, Halley knew that Kepler’s Third Law of Planetary Motion set out the distance between Earth and the sun in theoretical terms as, 1AU = rVenus ÷ 0.28 which meant that if the distance from Earth to Venus, rVenus, could be calculated, then the distance from Earth to the sun was easily deduced, a matter of simple division. Crucial to the calculation of rVenus is to find the value for the angle α which forms between observers’ lines of sight while charting Venus’ travel across the face of the sun, something which only happens during a rare astronomical event known as the Transit of Venus. See Figure 1. Figure 1 Figure 1 shows two observers positioned on opposite sides of the Earth, busily surveying Venus’ movement across the sun’s face. Their lines of sight converge at a vertex point, or point of intersection, on Venus, then move beyond it to the sun. Due to the principle of vertical angles, which stipulates that angles which share the same vertex point also share the same angle measurement, we know that the angle α that’s formed between Observer A and B‘s lines of sight is of the same value between Earth and Venus as it is between Venus and the sun. Once a is determined, its numerical value can be plopped into an equation we’ve been working with for some time now in this blog series. It’s similar to the equation previously used to calculate Earth’s distance to the moon, r = d x tan(θ) Follow this link to Optically Measuring Cosmic Distances for a review. And here is that equation with terms modified to reflect our new quest, the distance from Earth to Venus, rVenus = d ÷ tan(α) As for the variable d, the distance between the two observers, we’ve worked with that before, too. Follow this link to Determining Chord Length on Circle Earth for a refresher. Next time we’ll see how Venus’ travel path is key to determining the angle α, shown in green on the illustration, and how this angle is crucial to our discovery of the distance between Earth and the sun.
____________________________________
|
The Transit of Venus from Different Perspectives
Wednesday, June 3rd, 2015|
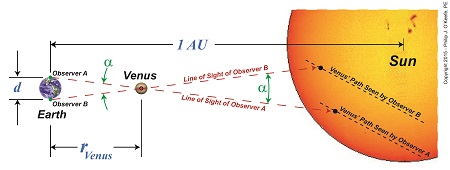
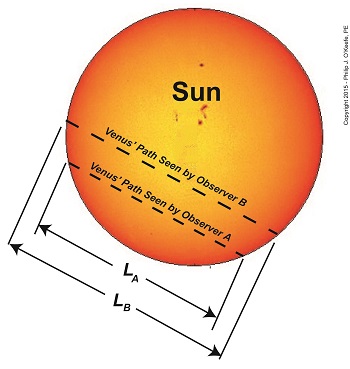
We’ve been working on calculating Earth’s distance to the sun and discussing how past scientists, including Johannes Kepler and Edmund Halley, contributed to the discussion. Today we’ll see how Halley used his theory on the transit of Venus together with Kepler’s Third Law of Planetary Motion and combined them with known mathematical principles to solve the riddle of this enormous distance, known as one astronomical unit, or AU. Halley’s solution began with stationing two observers with telescopes aimed at Venus on opposite sides of the Earth. Their different lines of sight would cause the principle of parallax to come into play, resulting in them seeing Venus from different perspectives. Their sight would converge at Venus’ center and an angle, α, would form between them. Halley posited that if this angle could be measured, it would be an important first step in calculating the distance between Earth and the sun. See Figure 1. Due to their differing perspectives, Observer A would see Venus traveling a path lower on the sun’s face, while Observer B would see it following a path higher up. See Figure 2. The net result was that the length, LA, of Venus’ path as seen by Observer A was significantly shorter than length, LB, of Venus’ path as seen by Observer B. Because of this, Observer B would have seen Venus pass in front of the sun before Observer A. These differing observations meant that even if both observers were to set their telescopic crosshairs on Venus at the exact same moment it became visible to each of them, it would serve no purpose, because they lacked a common point of reference at which to aim in order to take measurements. This fact made measuring the angle α with a physical device such as a protractor impossible. So Halley gave up on the idea of physically measuring α. Instead, he proposed calculating it based on the time it took for Observers A and B to watch Venus traverse the sun’s face from one side to the other along each of their observational paths. Next time we’ll see how Halley put his idea to work to calculate α and used it in conjunction with Kepler’s Third Law to calculate the AU.
____________________________________
|
The Astronomical Unit — It’s So Relative
Thursday, May 7th, 2015|
Last time we learned that early scientists used the Earth itself as an optical rangefinder to gauge its distance to the moon, and we posed the question: Can Earth be used in the same way to gauge distance to the sun? Unfortunately not. As we learned earlier in this blog series, the more distant the object, the larger the rangefinder that’s required, and the Earth just plain isn’t big enough to be used to compute that distance. The sun is 390 times farther away than the moon is, and that presents a real problem. Today we’ll learn about an alternate method to gauge this great distance. Johannes Kepler made a great contribution towards finding Earth’s distance to the sun when he developed his Third Law of Planetary Motion. Through his observation of planetary movements he was able to determine each planet’s relative distance from the sun in terms of what he dubbed the astronomical unit (AU), a yardstick by which the distance between all planets in our solar system and our shared sun could be judged. Kepler established the distance between Earth and the sun to be that astronomical unit, depicted in the illustration as r. The reason Kepler developed the AU was because in his day there was no known way to measure the distance to the sun. The AU, an abstract term with no real numerical value in terms of the distance being measured became a sort of placeholder term until r could actually be measured. The best the AU could do was allow him to determine how far a planet was from the sun relative to Earth’s distance from it. For example, his Third Law states that Venus’ distance to Earth is approximately one-quarter the distance between Earth and the sun, or 0.28 AU. That meant that Venus’ distance to the sun was three-quarters the distance of Earth to the sun, or 0.72 AU. Together, these two distances equaled one AU, the as yet unquantifiable distance r between Earth and the sun. Why all the fuss over Venus? Because Edmund Halley, a scientist who came after Kepler and shared in his fascination with interplanetary distances, would use Venus’ proximity to Earth to set up an optical rangefinder relationship between them and the object of his fixation, the sun. Crucial to this accomplishment would be making use of Venus’ orbital movement and the moment it would come into a direct line between Earth and the sun. We’ll explore that further next time.
____________________________________
|
Determining Chord Length on Circle Earth
Tuesday, April 28th, 2015|
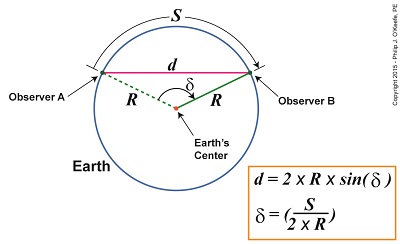
Last time we learned that early scientists used Earth as a huge optical rangefinder to gauge the distance, r, between it and the moon. But before they could put to use our by now very familiar distance calculating formula they needed to first determine the distance, d, between their observation positions. This distance is known within mathematical circles as a chord and is represented by the pink solid line in Figures 1 and 2. A chord is simply a straight line drawn between any two points on a circle, in this case the distance, d, between our observers of the moon. Its length can be determined mathematically if the Earth’s radius, R, and the curved distance, S, between Observers A and B are known. Calculating d was done with relative ease by putting Earth’s circular geometry and principles of mathematics to use. The formula that will accomplish this is shown in Figure 2’s inset box. And here’s the distance calculating formula, yet again: r = d × tan(θ) Figure 2 You will note that Figure 2 features a new symbol, δ , which represents a new angle, and a new trigonometric term, sin( ), or sine. To understand how the angle δ is formed, imagine a green line of length R that extends from Earth’s center to its surface. This is Earth’s radius, as determined by Eratosthenes. The end attached to Earth’s center pivots to allow R‘s other end to travel along Earth’s surface. It travels a path between Observers A and B, represented by curved line S. The angle δ is formed between the dashed green line, which represents R‘s starting point, and R‘s solid green line, which represents its finishing point at Observer B’s location. Figure 2 shows that the angle δ is calculated by dividing S by 2 × R . This numerical value is then entered into a scientific calculator, and when we press the sin button we’re provided with the sine value for angle δ. It should be noted that this is measured in radians, a measuring system typically associated with circles (rather than the more familiar degrees), in order to obtain the correct answer for d. Scientific calculators easily switch between the two modes. Follow this link if you’d like to learn more about radians. Now the Earth is relatively close to the moon, a mere 238,900 miles, and using it as an optical rangefinder to gauge distance to the moon is relatively straightforward. But can it be used to judge the distance to its sun, a whopping 93,000,000 miles away? We’ll see next time why it can’t and what alternate method must be used.
____________________________________
|
Optically Measuring Cosmic Distances
Wednesday, April 22nd, 2015|
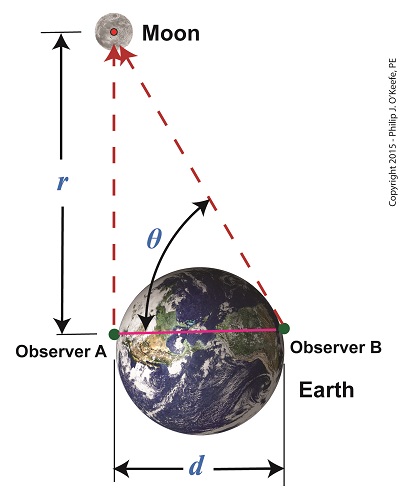
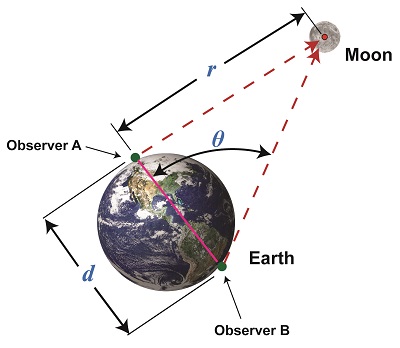
Last time we learned that the bigger an optical rangefinder, the better its accuracy in measuring distant objects. Today we’ll take that concept a step further when we discover how Earth itself was used by ancient scientists to gauge its distance to the moon. Today’s blog will be strewn with embedded links to past blogs in this series, all of which have been building up to our understanding of gravity, a complex subject with many pieces to its puzzle. There are a few remaining pieces to be placed which will be covered in future blogs, but I promise we’ll get there. Long before Edmund Halley’s time, scientists used the Earth as a huge optical rangefinder. In doing so they employed the principles of parallax and trigonometry to obtain reasonably accurate measurements of the distance between Earth and its nearest neighbors, starting with the moon. See Figure 1. The illustration shows how it was done. Two observers armed with telescopes viewed the moon from opposite sides of the earth. Their lines of sight are represented by dashed lines, and together with the solid pink line which represents the distance between them, d, a right triangle was formed. Because Observer B was situated on the other side of the globe, his line of sight fell at an angle relative to Observer A’s, due to the Principle of Parallax. The angle that formed at the point in the triangle at which B was situated we’ll call θ. The fact that a right triangle was formed at Observer A’s observation point will enable our ancient scientists to use principles of trigonometry and parallax in their quest to find the distance to the moon. Follow this link to a refresher blog on the subject, Using Parallax to Measure Distance. At precisely the same moment the moon moved into Observer A’s telescopic line of sight, Observer B adjusted his telescope to center the moon within it. Observer B then duly measured the angle θ formed with a protractor, just as would be done with a rangefinder. If you’ve been reading along in this series, this setup might look familiar to you. In fact, the two mirrors of a military optical rangefinder work in exactly the same way as our two observers looking at the moon. Follow this link to a refresher on the internal workings of a rangefinder. Once the angle θ’s value had been determined, it was used to calculate the distance r between Earth and the moon with the same equation we’ve been using to measure distances using military optical rangefinders: r = d × tan(θ) As far as our moon observers go, the only variable left for them to determine before they are able to measure Earth’s distance to the moon is d, the distance between their viewing positions on Earth. We’ll see how to solve for d next time, when we put the Earth’s geometry to work for us.
____________________________________
|