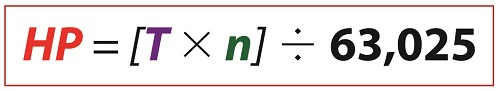Archive for the ‘Personal Injury’ Category
Friday, March 2nd, 2018
|
Last time we discussed how the curved features of a centrifugal pump are key to its functionality. Today we’ll examine a centrifugal pump’s impeller action and see how it creates a volatile environment inside the pump in which cavitation bubbles flourish.

Centrifugal Pump Impeller Action
Inside a centrifugal pump both low and high pressure areas are created, chiefly due to the action of the pump’s spinning impeller. Low pressure is created at the water inlet in a way very similar to what happens when you pull the plug on your bathtub. With the plug removed the drain opens and a tiny whirlpool forms, causing water to get sucked into the plumbing for discharge.
The same thing happens inside a centrifugal pump due to tumultuous internal water movement. The spinning impeller vigorously moves water from inlet to discharge. As water is discharged, a void, or vacuum, is created inside the pump, causing water at the inlet to get sucked inside at low pressure, very much like when you suck liquid through a straw.
As water moves inside the housing, it comes into contact with the rotating impeller itself. This impeller is comprised of multiple spiral curved blades with a volute shape, made to maximize efficient movement of water. They use the power of centrifugal force to create a high pressure environment, and water is flung at high speed towards the pump’s outlet, where it is then discharged.
Next time we’ll see how the coexistence of low and high pressures within the centrifugal pump housing create the problem of cavitation bubbles.
opyright 2018 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: cavitation bubbles, centrifugal pump, discharge, impeller, impeller blades, inlet, volute
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Centrifugal Pump Impeller Action
Wednesday, February 21st, 2018
|
Last time we learned how centrifugal pumps can create a low pressure environment at the pump’s inlet, which can allow water inside the pump to boil at temperatures far lower than normal. Ultimately, this results in the formation of tiny but destructive cavitation bubbles. Today we’ll see how a centrifugal pump’s curved features are key to its functionality.
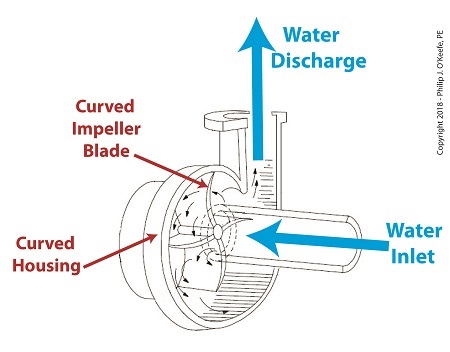
A Centrifugal Pump’s Curved Features are Key to Functionality
Even a casual glance at a centrifugal pump will disclose its many curved features. As the illustration shows, both the housing and internal impeller blades, are curved. These curves are known as volutes. The volutes’ dimensions are mathematically generated by engineers to facilitate the precise flow of water from inlet to discharge by way of the pump’s impeller blades.
Next time we’ll see how a centrifugal pump is home to both low and high water pressure, creating a volatile environment in which cavitation bubbles form and collapse.
opyright 2018 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: cavitation, centrifugal pump, engineering, flow, housing, impeller blades, volute
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on A Centrifugal Pump’s Curved Features are Key to Functionality
Sunday, January 28th, 2018
|
Last time we learned how the thermodynamic properties of water contribute to the phenomenon of cavitation, and how liquids exist in three states, solid, liquid, or vapor, depending on temperature and surrounding air pressure. Our example of an open pot of water being heated on a stove demonstrated that once water temperature rose above 212ºF, it changed to steam, which initiated the cavitation process. Today we’ll see how decreasing pressure contributes to cavitation.
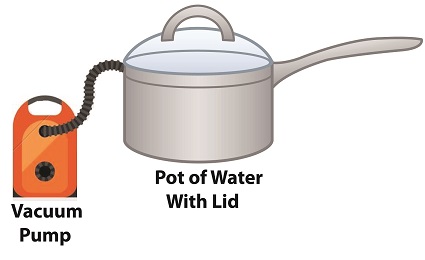
How Decreasing Pressure Contributes to Cavitation
Cavitation can occur without a heat source. In our pot example, we can start the cavitation process by simply decreasing the pressure of the air resting on top of the water, thereby also decreasing the water’s pressure.
Normally atmospheric pressure on Earth exists at around 15 pounds per square inch (PSI). But if we introduce a vacuum pump to an enclosed space, we can create an internal pressure which is lower than the surrounding atmospheric pressure outside the pot. In other words, we create a vacuum. A vacuum is any air pressure lower than atmospheric pressure. This vacuum environment produces an entirely new set of circumstances under which cavitation can occur. In fact, creating a vacuum makes it possible to boil water without using any heat!
As we learned in a past blog on the different forms of heat energy, the boiling point of water varies depending on the location of the stovetop, whether it’s in a place of low altitude, like New Orleans, or higher altitude, like Denver. But if we apply a tight lid to the pot and isolate its internal atmosphere from surrounding atmospheric pressure, you create a closed environment. This allows us to manipulate the pot’s internal pressure. When we attach a vacuum pump to remove air, we reduce the air pressure bearing down on the water inside. With much of the air removed, pressure inside the pot drops below normal atmospheric pressure existing outside the pot, and we discover that at 0.25 PSI water turns to steam at a mere 59ºF and cavitation can begin. That’s right, you can boil water without using heat.
Next time we’ll apply our knowledge of water pressure and temperature to an industrial setting and see how cavitation occurs inside pumps.
opyright 2018 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: atmospheric pressure, cavitation, temperature, thermodynamics, vacuum
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on How Decreasing Pressure Contributes to Cavitation
Monday, January 15th, 2018
|
Last time we introduced the phenomenon of cavitation, which simply stated is the rapid formation and collapse of vapor bubbles within liquids. It’s a destructive force that eats away at the metal parts of water pumps, used in power plants and other industrial settings. To understand how cavitation comes into play, we’ll explore a branch of engineering known as thermodynamics.
Cavitation doesn’t occur in a glass of water resting on a counter, but bring that water to a boil and the cavitation process will begin. That’s because cavitation is initiated when liquids change form from one physical state to another, in this case from a liquid to a vapor we commonly call steam. All liquids exist in three states, namely solid, liquid, and vapor, but in our thermodynamic analysis we’ll only consider two, liquid and vapor, because cavitation can’t occur in solids.

Thermodynamic Properties of Water and Cavitation
At normal atmospheric pressure of 15 pounds per square inch (PSI) which exists in the average kitchen, water remains in a liquid state between the temperatures of 32ºF and 212ºF. Above 212ºF water begins to boil, transforming into steam vapor. The state in which water exists depends on two thermodynamic properties, namely temperature and pressure. Change one of these variables and it affects the other, and thereby the conditions under which cavitation will occur.
We’ll take an in-depth look at this next time when we revisit the topics of pressurization and vacuums.
opyright 2018 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: cavitation, engineering, power plants, pumps, states of water, thermodynamics
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on Thermodynamic Properties of Water and Cavitation
Wednesday, January 3rd, 2018
|
Shortly after I graduated with my engineering degree I worked as a power plant engineer at an electric utility. One day I was walking through the plant and heard a loud racket coming from the boiler feel pumps. These are the massive centrifugal pumps that deliver pressurized water to the boiler. The water is transformed into steam to drive steam turbines and spin electrical generators, which ultimately results in electrical power. The noise was so loud, it sounded like rocks were being ground up. I asked a coworker what was going on, and he replied matter-of-factly, “The pumps are cavitating.”

Boiler Feed Pumps Experience Cavitation
So what exactly is cavitation? We’ll find out next time when we explore the mechanics of this noisy phenomenon as it applies to boiler feed pumps and other centrifugal pumps.
opyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: boiler, boiler feed pumps, cavitation, centrifugal pump, electric utility, electrical generator, engineering, power plant, steam turbine
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, power plant training, Product Liability | Comments Off on Boiler Feed Pumps Experience Cavitation
Thursday, December 21st, 2017
|
Last time we had a look inside a marvelous piece of engineering machinery known as a crankshaft. It plays a key role in converting the reciprocating linear motion of a steam driven engine into the rotary motion required to power externally mounted devices that are attached to it. Today we’ll finish up our blog series on flywheels when we see how using one in conjunction with a crankshaft facilitates a more even transmission of energy. Reciprocating engines maximize efficiency when they employ flywheels.
We learned that the energy in the steam supply decreases as the piston moves in its cylinder, which means a concurrent decrease in the engine’s horsepower and its ability to power machinery. Without an intervening action, the reciprocating steam engine would stall. Now, let’s see how adding a flywheel to the crankshaft can solve the problem.
Reciprocating Engines Maximize Efficiency When They Employ Flywheels
As we’ve learned before, a flywheel stores up kinetic energy while the engine powering it is performing at full horsepower, but if that power should drop off or cease to be produced, the flywheel gives up the kinetic energy stored inside it so as to keep externally mounted machinery operating until that stored energy is exhausted. This is all made possible because flywheels are designed to have moments of inertia sufficient to positively contribute to its storage of kinetic energy. This inertia is a numerical representation of the flywheel’s resistance to change in motion. Please review our past blog on the subject to refresh your memory.
The overall effect is that while the engine is operating, there’s an even flow of energy between the engine and flywheel and horsepower is supplied to keep machinery mounted to the crankshaft operating. Any diminishment in the power supplied will be compensated for by the flywheel’s stored kinetic energy.
Next time we’ll introduce a new topic, a phenomenon known as cavitation.
opyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: crankshaft, efficiency, engineering, flywheel, horsepower, kinetic energy, moment of inertia, reciprocating steam engine
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Reciprocating Engines Maximize Efficiency When They Employ Flywheels
Friday, December 15th, 2017
|
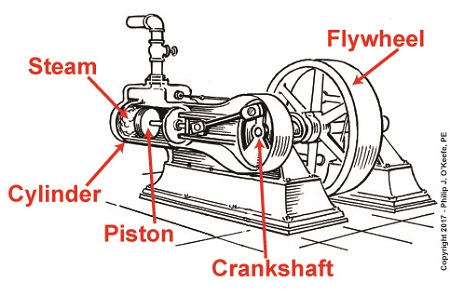
Last time, we learned that a crankshaft is an engineering device which converts the reciprocating linear motion of an engine’s back-and-forth moving piston into the rotary motion that powers externally attached machinery. Its movement is shown here,

A Crankshaft in Motion
We’ll see how a crankshaft and piston’s motion benefits by the use of a flywheel next time.
opyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: crankshaft, cylinder, engine, engineering, flywheel, machinery, piston, reciprocating linear motion, rotary motion
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on A Crankshaft in Motion
Wednesday, December 6th, 2017
|
Last time we developed an engineering formula to calculate the horsepower required to accelerate a flywheel by way of a reciprocating steam engine, which contributes to the storage of kinetic energy inside a flywheel. Today we’ll gain a clearer understanding of how this works when we take a look inside a reciprocating steam engine.
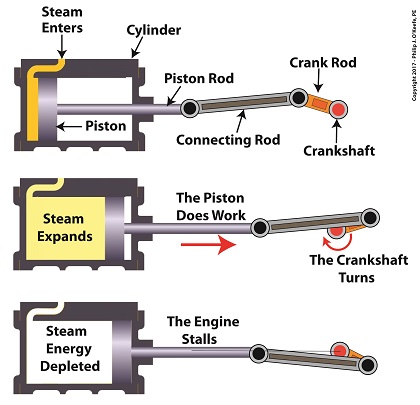
A Look Inside a Reciprocating Steam Engine
A reciprocating steam engine performs the work of transforming steam’s heat energy into the mechanical energy needed to move a piston contained within a cylinder. During a complete operating cycle this piston travels from one end of the cylinder to the other, then back again. This is made possible because during the first half of the cycle pressurized steam enters one end of the cylinder and expands inside it, forcing the piston to move.
This process inside the cylinder results in movement of a piston that’s attached to a piston rod, which in turn is connected to a crankshaft via a connecting rod and crank rod. The crankshaft is a device which converts the reciprocating linear motion of an engine’s piston into rotary motion and in so doing facilitates the powering of any externally mounted rotating machinery attached to it. So long as there’s ample steam to power the internal piston, over time, energy in the form of horsepower will be available to externally mounted devices. The energy in the steam decreases as the steam expands behind the moving piston. So, the engine’s horsepower, will decrease as the piston travels to the end of the cylinder. If the energy in the steam should become depleted, the reciprocating steam engine will stall. The engine will no longer be able to perform work.
Next time we’ll see how a crankshaft works when we take a look inside it.
opyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: connecting rod, crank rod, crankshaft, energy, engineering, flywheel, kinetic energy, piston rod, power, reciprocating steam engine, work
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on A Look Inside a Reciprocating Steam Engine
Friday, November 24th, 2017
|
Last time we discussed how torque is created as a flywheel spins. This torque is a factor of the flywheel’s moment of inertia, which is dependent on how far the masses of the flywheel’s parts are located from its center of rotation. Today we’ll present a formula to compute how much horsepower is required to accelerate a flywheel. And here it is,
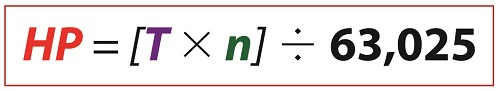
Horsepower Required to Accelerate a Flywheel
where, T is the torque created on the flywheel’s shaft in units of inch-pounds. The term n is the flywheel shaft’s speed of rotation in revolutions per minute, RPM. Horsepower, HP, is engineering shorthand for a unit of power equal to 6600 inch-pounds per second, and the number 63,025 is a constant needed to convert torque, T, and the spinning shaft’s rotations per minute, RPM, into horsepower units.
Torque is present whether the flywheel’s spin accelerates or decelerates. During acceleration torque is created, which contributes to the production of kinetic energy that’s stored inside the flywheel. When a flywheel’s spin decelerates, its mass experiences the effects of negative acceleration, and stored kinetic energy is released.
As we learned awhile back, horsepower is a function of torque in any moving machinery, including engines and flywheels. An engine must produce horsepower to accelerate a flywheel connected to its shaft. By the same token, when the engine’s horsepower output diminishes or stops, the flywheel begins to decelerate. This deceleration causes kinetic energy stored within the flywheel to be released, providing horsepower necessary to keep the engine and flywheel spinning. That is, until the power output of the engine returns or the stored kinetic energy of the flywheel is ultimately exhausted.
We’ll see how that works next time when we take a look inside a reciprocating engine.
opyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: acceleration, deceleration, engine, engineering, flywheel, horsepower, kinetic energy, mass, moment of inertia, torque
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Horsepower Required to Accelerate a Flywheel
Monday, November 13th, 2017
|
Last time we began our discussion on moment of inertia and how it affects a flywheel’s storage of kinetic energy. That inertia is a function of the flywheel’s mass, in particular how the mass is distributed. Today we’ll continue our discussion and see how an engineering principal known as torque affects things.

Flywheel Torque and Distribution of Mass
We learned in a previous blog that torque is most simply defined as a measure of how much force acts upon an object to cause it to rotate around a pivot point or center of rotation, shown as a small black dot in the illustration. For our discussion we’ll focus on two parts of the flywheel, the hub, part A, and the rim, part E.
Part A has a mass mA located a distance rA from the flywheel’s center, while part E has a mass mE located a distance rE from it. When an engine applies mechanical power to the flywheel by way of its rotating shaft, the revolutions per minute, RPM, increase and along with it the angular velocity, ω, also increases. For a refresher on this, follow the link.
Because of this relationship, we can calculate the kinetic energy contained within a flywheel using the kinetic energy formula,
KE = ½ × ∑[m × r2] × ω2 (1)
As the flywheel’s angular velocity increases or decreases in response to the engine’s energy output, parts A and E reflect acceleration or deceleration of aA and aE. Since parts A and E exhibit both mass and acceleration, they are subject to Newton’s Second Law of Motion, which states that force equals mass times acceleration. Using that relationship we can calculate the force exerted on each part by,
FA = mA × aA (2)
FE = mE × aE (3)
Part A is small compared to part E, therefore mE is greater than mA and accordingly FE is greater than FA. Forces FA and FE act as torques, because they cause parts A and E to rotate around the flywheel’s center of rotation, so they are designated as Torque A, TA, and Torque E, TE. These torques are computed by,
TA = FA × rA (4)
TE = FE × rE (5)
Part E’s greater mass will contribute more torque than part A, and it will also contribute more to the flywheel’s kinetic energy content.
Most flywheels are designed with heavy rims supported by small hubs and slender spokes, because the more mass that’s distributed away from the flywheel’s center of rotation, the greater the flywheel’s moment of inertia and torque, and the more kinetic energy it can store.
Next time we’ll develop an equation which allows us to quantify the horsepower required to accelerate a flywheel.
opyright 2017 – Philip J. O’Keefe, PE
Engineering Expert Witness Blog
____________________________________ |
Tags: distribution of mass, engineering, flywheel, kinetic energy, mass, moment of inertia, torque
Posted in Engineering and Science, Expert Witness, Forensic Engineering, Innovation and Intellectual Property, Personal Injury, Product Liability | Comments Off on Flywheel Torque and Distribution of Mass